The Expert Physics and Math Blog
Schrödinger’s Cat and the Qbit
/27 Comments/in Physics Articles/by Mark StuckeyThe concept of quantum superposition (or superposition for short) is very counterintuitive, as Schr##\ddot{\text{o}}##dinger noted in 1935 writing [1], “One can even set up quite ridiculous cases.” To make his point, he assumed a cat was closed out of sight in a box with a radioactive material that would decay with 50% probability within an…
Trending Articles
Recent Entries

The Slinky Drop Experiment Analysed
/
1 Comment
The slinky drop is a rather simple experiment. In its most basic form, it requires only a popular toy for children, a stable hand, and a keen eye.…
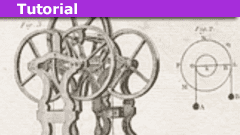
How to Solve a Multi-Atwood Machine Assembly
IntroductionThe figure on the right shows a "double-double" Atwood machine with three ideal pulleys and four masses. All pulleys are released from…

The Lambert W Function in Finance
Preamble
The classical mathematician practically by instinct views the continuous process as the "real" process, and the discrete process as an approximation…

Why Division by Zero is a Bad Idea
A division by zero is primarily an algebraic question. The reasoning therefore follows the indirect pattern of most algebraic proofs:
What if it was allowed?
Then…
Digital Filtering and Exact Reconstruction of Digital Audio
Introduction
This elaborates some of the claims in my insights article on digital audio.
The Sinc Function
The first link in my insights article has…

Introduction to Digital Audio
IntroductionFirst, we need some background in Digital Signals. This can be mathematically quite advanced, but since I would like this…
Series in Mathematics: From Zeno to Quantum Theory
Introduction
Series play a decisive role in many branches of mathematics. They accompanied mathematical developments from Zeno of Elea (##5##-th century…
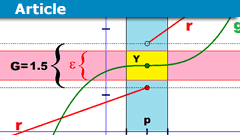
Epsilontic – Limits and Continuity
Abstract
I remember that I had some difficulties moving from school mathematics to university mathematics. From what I read on PF through the years, I…

The Poor Man’s Milli-Ohm Meter
Introduction
In a previous article on measuring battery internal resistance, a simple technique for low-resistance measurement was outlined. In this article,…

Differential Equation Systems and Nature
Abstract
"Mathematics is the native language of nature." is a phrase that is often used when it comes to explaining why mathematics is all around in natural…

Beginners Guide to Precalculus, Calculus and Infinitesimals
Introduction
I am convinced students learn Calculus far too late. In my view, there has never been a good reason for this.In the US, they go through…

How to Apply Newton’s Second Law to Variable Mass Systems
Introduction
The applicability of Newton's second law in the oft-quoted "general form" $$\begin{align}\frac{d\mathbf{P}}{dt}=\mathbf{F}_{\text{ext}}\end{align}$$…

What Are Numbers?
Introduction
When doing mathematics, we usually take for granted what natural numbers, integers, and rationals are. They are pretty intuitive. Going…

Introduction to the World of Algebras
Abstract
Richard Pierce describes the intention of his book [2] about associative algebras as his attempt to prove that there is algebra after Galois…

Why ChatGPT Is Not Reliable
I'll start with the simple fact: ChatGPT is not a reliable answerer of questions.To try to explain why from scratch would be a heavy lift, but fortunately,…

What Are Infinitesimals – Simple Version
Introduction
When I learned calculus, the intuitive idea of infinitesimal was used. These are real numbers so small that, for all practical purposes (say…

How Quantum Information Theory Solves “the only mystery” of Quantum Mechanics
In Chapter 37 of "The Feynman Lectures on Physics Volume 1," Richard Feynman famously wrote that the mystery of wave-particle duality in the double-slit…

What Are Infinitesimals – Advanced Version
Introduction
When I learned calculus, the intuitive idea of infinitesimal was used. These are real numbers so small that, for all practical purposes (say…

Opinion: When Pro Scientists Explain Using Pop Science
Abstract
There is so much to say about the many endeavors by professional scientists to explain to us the world. The list is long: Carl Sagan, Harald…

The Art of Integration
Abstract
My school teacher used to say
"Everybody can differentiate, but it takes an artist to integrate."
The mathematical reason behind this phrase…

A Lesson In Teaching Physics: You Can’t Give It Away
A central principle of Physics Forums regarding homework help is not to provide solutions on demand but to guide students along a path to the answer. The…

An Overview of Complex Differentiation and Integration
Abstract
I want to shed some light on complex analysis without getting all the technical details in the way which are necessary for the precise treatments…
How to Measure Internal Resistance of a Battery
Introduction
A commonly encountered school-level Physics practical is the determination of the internal resistance of a battery - typically an AA or D…

When Lie Groups Became Physics
Abstract
We explain by simple examples (one-parameter Lie groups), partly in the original language, and along the historical papers of Sophus Lie, Abraham…

Why There Are Maximum Mass Limits for Compact Objects
In this article, we will look at why there are maximum mass limits for objects that are supported against gravity by degeneracy pressure instead of kinetic…

Oppenheimer-Snyder Model of Gravitational Collapse: Implications
Part 1: OverviewPart 2: Mathematical DetailsPart 3: ImplicationsIn the last article in this series, we finished up with a metric for the Oppenheimer-Snyder…

What Are Tensors and Why Are They Used in Relativity?
If you try learning general relativity, and sometimes special relativity, on your own, you will undoubtedly run into tensors. This article will outline…

Oppenheimer-Snyder Model of Gravitational Collapse: Mathematical Details
Part 1: OverviewPart 2: Mathematical DetailsPart 3: ImplicationsIn a previous article, I described in general terms the model of gravitational…

When Discussing the Twin Paradox: Read This First
This article is intended for anyone who wants to start a thread here at Physics Forums on the twin paradox. There are already many, many threads here on…

The Oppenheimer-Snyder Model of Gravitational Collapse: An Overview
Part 1: OverviewPart 2: Mathematical DetailsPart 3: ImplicationsMost people who have spent any time at all studying GR are familiar with the…

Subtleties Overlooked in Friction Questions: Object Slides Down Ramp
Problem statement (simplified)
An object slides down a ramp at angle θ to encounter level ground. Both surfaces have kinetic friction: μ' on the ramp,…
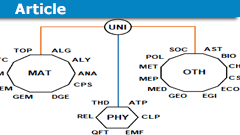
Classification of Mathematics by 42 Branches
I often read questions about our classification scheme that we use on physicsforums.com to sort posts by science fields and subjects, what has…

Reduction of Order For Recursions
This is not meant as a full introduction to recursion relations but it should suffice for just about any level of the student.Most of us remember recursion…

Counting to p-adic Calculus: All Number Systems That We Have
An entire book could easily be written about the history of numbers from ancient Babylon and India, over Abu Dscha'far Muhammad ibn Musa al-Chwarizmi (##\sim…

Évariste Galois and His Theory
* Oct. 25th, 1811 † May 31st, 1832
... or why squaring the circle is doomed.
Galois died in a duel at the age of twenty. Yet, he gave…
Yardsticks to Metric Tensor Fields
I asked myself why different scientists understand the same thing seemingly differently, especially the concept of a metric tensor. If we ask a topologist,…

Programming an ATmega8A using Arduino
If you are interested in programming and electronics, you probably do not need an introduction to Arduino. If you want to make your Arduino projects permanent,…
P vs. NP and what is a Turing Machine (TM)?
P or NP
This article deals with the complexity of calculations and in particular the meaning of
##P\stackrel{?}{\neq}NP##
Before we explain what P and…

Quantum Computing for Beginners
Introduction to Quantum Computing
This introduction to quantum computing is intended for everyone and especially those who have no knowledge of this relatively…
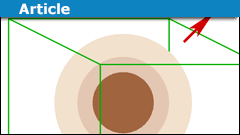
A Physics Misconception with Gauss’ Law
Introduction
It is relatively common to see the following type of argument:
The surface area is ##A## and the enclosed charge is ##Q##. The electric…
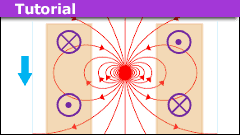
How to Model a Magnet Falling Through a Conducting Pipe
Introduction
In an earlier article, we examined a magnet falling through a solenoid. We argued that the point dipole model can account for the basic features…
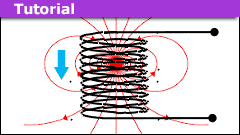
How to Model a Magnet Falling Through a Solenoid
Introduction
Modeling a magnet realistically is a task best done numerically. Even the simplified model of two separated disks with uniform surface…

How Can We Jump When the Ground Does No Work?
It is relatively common on Physics Forums to see arguments that are effectively similar to the following:
When we jump off the ground, the ground does…
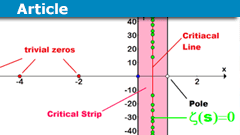
The History and Importance of the Riemann Hypothesis
Riemann Hypothesis History
The Riemann Hypothesis is one of the most famous and long-standing unsolved problems in mathematics, specifically in the field…
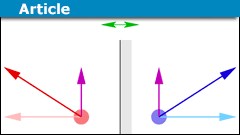
Symmetry Arguments and the Infinite Wire with a Current
Many people reading this will be familiar with symmetry arguments related to the use of Gauss law. Finding the electric field around a spherically symmetric…

Parallel Programming on a CPU with AVX-512
This article is the second of a two-part series that presents two distinctly different approaches to parallel programming. In the two articles, I use different…

Parallel Programming on an NVIDIA GPU
This article is the first of a two-part series that presents two distinctly different approaches to parallel programming. In the two articles, I use different…

A Novel Technique of Calculating Unit Hypercube Integrals
Introduction
In this insight article, we will build all the machinery necessary to evaluate unit hypercube integrals by a novel technique. We will first…
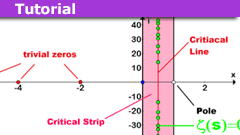
The Extended Riemann Hypothesis and Ramanujan’s Sum
Riemann Hypothesis and Ramanujan's Sum ExplanationRH: All non-trivial zeros of the Riemannian zeta-function lie on the critical line.
ERH: All…
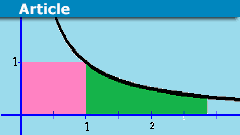
The Amazing Relationship Between Integration And Euler’s Number
We use integration to measure lengths, areas, or volumes. This is a geometrical interpretation, but we want to examine an analytical interpretation that…

Superdeterminism and the Mermin Device
Superdeterminism as a way to resolve the mystery of quantum entanglement is generally not taken seriously in the foundations community, as explained in…

