- #1
Artlav
- 162
- 1
I'm trying to make sense of the way time dimension is related to the other 3, the example is twin paradox:
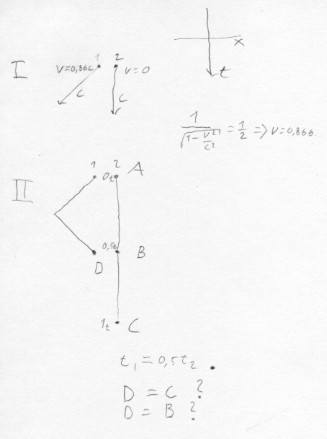
Observer 1 is moving away at 0.866c from observer 2, who is standing still, then turns around at a defined point and goes back at the same speed, arriving back to observer 2 position, and see him 0.5t older than classically expected.
Now, the problem with that visualization is why are the points D and C are the ones that are in the same "now"?
Why does 1 not arrive at point B instead and see the 2 at 0.5t also?
Are the points B and D not at the same space&time coordinates?
Alternatively, why, if C and D are the same, can they see each other?
Because it implies that things could be seen across a distance in time dimension, which contradicts the fact that we don't see our past and future trailing around us, and things can't be seen in two places at once.
Or, is there something fundamentally wrong with that visualization attempt?
.
Observer 1 is moving away at 0.866c from observer 2, who is standing still, then turns around at a defined point and goes back at the same speed, arriving back to observer 2 position, and see him 0.5t older than classically expected.
Now, the problem with that visualization is why are the points D and C are the ones that are in the same "now"?
Why does 1 not arrive at point B instead and see the 2 at 0.5t also?
Are the points B and D not at the same space&time coordinates?
Alternatively, why, if C and D are the same, can they see each other?
Because it implies that things could be seen across a distance in time dimension, which contradicts the fact that we don't see our past and future trailing around us, and things can't be seen in two places at once.
Or, is there something fundamentally wrong with that visualization attempt?
.