- #1
maker2807
- 3
- 0
Hi, I am new to this forum so hello to everybody. I have this problem to solve:
Q is moving away from P at speed 4/5 c. After 3 years (in Q's frame of reference) he turns around (assuming that turning takes no time) and is moving back to P at speed 4/5 c.
What are spacetime intervals between:
(A) Start and turn
(B) Turn and arriving back
(C) Start and arriving back
c = speed of light
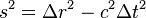
I suppose that problem isn't very difficult, but I'm not sure about my solution. First of all, I'm not sure if I'm supposed to calculate s or s2. The second problem is, that I'm not sure if I should use t = 3 years (time in Q's frame of reference) or t = 5 years (time in P's frame of reference calculated from time dilatation formula).
For (A), I think that r = 4 ly (distance traveled at 4/5c for 5 years in P's frame of reference) and t is either 5 or 3 years. Then result should be easily obtained from the equation. Am I right?
For (B), I think it's the same as (A), because speed is the same as well as time. Or should I change the speed sign to minus because of different direction?
For (C) should the distance be zero because of event's occurring at the same place? And what about time? Should it be 6 years or 10 years?
Thanks in advance for your responses.
Homework Statement
Q is moving away from P at speed 4/5 c. After 3 years (in Q's frame of reference) he turns around (assuming that turning takes no time) and is moving back to P at speed 4/5 c.
What are spacetime intervals between:
(A) Start and turn
(B) Turn and arriving back
(C) Start and arriving back
c = speed of light
Homework Equations
The Attempt at a Solution
I suppose that problem isn't very difficult, but I'm not sure about my solution. First of all, I'm not sure if I'm supposed to calculate s or s2. The second problem is, that I'm not sure if I should use t = 3 years (time in Q's frame of reference) or t = 5 years (time in P's frame of reference calculated from time dilatation formula).
For (A), I think that r = 4 ly (distance traveled at 4/5c for 5 years in P's frame of reference) and t is either 5 or 3 years. Then result should be easily obtained from the equation. Am I right?
For (B), I think it's the same as (A), because speed is the same as well as time. Or should I change the speed sign to minus because of different direction?
For (C) should the distance be zero because of event's occurring at the same place? And what about time? Should it be 6 years or 10 years?
Thanks in advance for your responses.
Last edited by a moderator:
