- #1
brolaf
- 1
- 0
[Complex Analysis] Conformal mapping of a column into a line
I'm having a problem with this problem (:rofl:) where I have to transform an area of 2 circles, the one contained within the other, into a straight line.
I've managed to transform the circles using a Möbius transformation into a column bounded by 1/4<Re w<1/2 but I have no idea how to go further than that.. I know my teacher must have talked about this at some point, but I have no memory of it. Also, the course "book" we were given is just a printed handout of some 100 pages written by the teacher himself. While it covers alot, there are some gaps in it, including this.
It seems to me fairly illogical to be able to transfer a area into a straight line like this. I mean, one could of course make the column thinner so it would "look" like a line, but to transform it into an "true" infinitely thin line is beyond my comprehension of the subject. Still, I'm pretty new to this subject and I'm still having my first glances at a lot of things.. but any help with this would be greatly appreciated!
Find w that transforms:
{ z [itex]\in[/itex]ℂ |z| < 2 and |z-1| < 1 }
into:
{ z [itex]\in[/itex]ℂ Re z > |Im z| }
w1 = [itex]\frac{1}{2-z}[/itex]
I made this picture to describe the problem and my progress better:
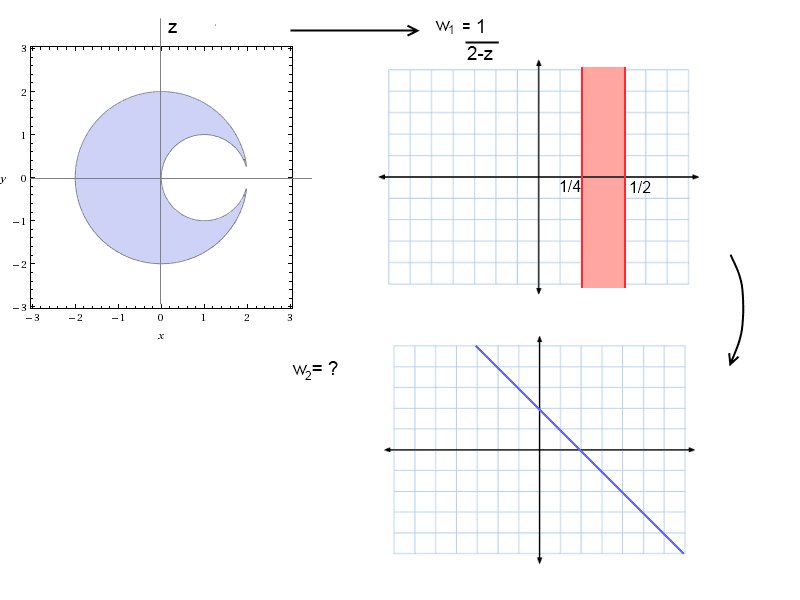
Cheers,
- brolaf
Homework Statement
I'm having a problem with this problem (:rofl:) where I have to transform an area of 2 circles, the one contained within the other, into a straight line.
I've managed to transform the circles using a Möbius transformation into a column bounded by 1/4<Re w<1/2 but I have no idea how to go further than that.. I know my teacher must have talked about this at some point, but I have no memory of it. Also, the course "book" we were given is just a printed handout of some 100 pages written by the teacher himself. While it covers alot, there are some gaps in it, including this.
It seems to me fairly illogical to be able to transfer a area into a straight line like this. I mean, one could of course make the column thinner so it would "look" like a line, but to transform it into an "true" infinitely thin line is beyond my comprehension of the subject. Still, I'm pretty new to this subject and I'm still having my first glances at a lot of things.. but any help with this would be greatly appreciated!
Homework Equations
Find w that transforms:
{ z [itex]\in[/itex]ℂ |z| < 2 and |z-1| < 1 }
into:
{ z [itex]\in[/itex]ℂ Re z > |Im z| }
The Attempt at a Solution
w1 = [itex]\frac{1}{2-z}[/itex]
I made this picture to describe the problem and my progress better:
Cheers,
- brolaf
Last edited: