What is the way to determine the current in DC circuit with R,L,C

tsw99

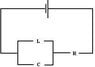
If I have a constant emf, then connect it to a resistor and an inductor and capacitor in parallel.

At the time when the switch is closed (I haven't drawn it), the voltage across L and across C should be the same since they are in parallel(?) (in fact it should be in any time later)

But there will be an induced emf across L, so the voltage across C should not be zero (but there is no charge on C!!! By V=Q/C, the voltage should be zero!).

So the initial current should not be E/R right? But from textbook, an uncharged cap should act as a short circuit, so no current passes through L. So what is the way to determine the initial current? (I believe the final current should be E/R because the fully charged cap acts as a open circuit)

I hope you understand what I am asking about.

Attached Thumbnails

 

truesearch

I agree withe your expression for the final current, the inductance acts a short circuit.
at switch on. Think that L and C will oscillate and eventually setle to your final values

AlephZero

For a physically sensible solution, you can't have a sudden jump in the current through the inductor, because that would generate an "infiinite" back EMF.

So immediately after you close the switch, the current through L must be the same as it was before, i.e. zero. Therefore you have an RC circuit connected to the battery, the initial current through R and C will be E/R, and the initial voltage across the capacitor (and the inductor) will be 0.

The same logic applies if you open the switch again. The current through L can't instantly change its value. Since no current will be flowing in R, for an ideal inductor and capacitor the current in the LC circuit would continue to oscillate for ever.

Of course that would not happen with real components, because there would always be some resistance R' in series with L. In that case, the initial oscillations would decay and leave a steady current of E/(R+ R') flowing through the resistor and the inductor.