- #1
peanutaxis
- 24
- 3
Hi, (this is not a homework question)
If I have a bicycle with COM, M (in line with the center of the wheels, C) on an incline, angle Φ, and the bicycle is NOT moving at all because the brake is on at B.
I am trying to put in the forces acting on the wheel. I figure that the weight of the bicycle is probably acting through the center of the wheel because the COM is at the same height (would this change if the COM was in a different place?). And because the wheel is not moving laterally I figure the friction force is opposing the weight, but acting at ground level.
The brake is preventing the wheel from turning CCW, and so I think the ?? force from the brake needs to also be mgsinΦ in a CW direction. But the problem is that if I put the brake/?? force in, the static/overall forces on the wheel won't balance and the wheel should move off in the direction of the ?? force.
Help!?
thanks
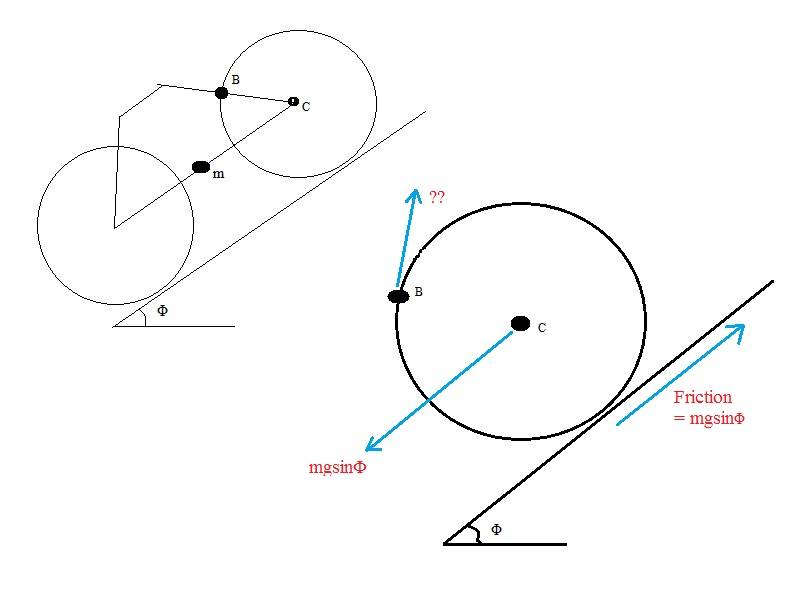
If I have a bicycle with COM, M (in line with the center of the wheels, C) on an incline, angle Φ, and the bicycle is NOT moving at all because the brake is on at B.
I am trying to put in the forces acting on the wheel. I figure that the weight of the bicycle is probably acting through the center of the wheel because the COM is at the same height (would this change if the COM was in a different place?). And because the wheel is not moving laterally I figure the friction force is opposing the weight, but acting at ground level.
The brake is preventing the wheel from turning CCW, and so I think the ?? force from the brake needs to also be mgsinΦ in a CW direction. But the problem is that if I put the brake/?? force in, the static/overall forces on the wheel won't balance and the wheel should move off in the direction of the ?? force.
Help!?
thanks