2D Vectors - Addition and Subtraction of Successive Displacement Vectors

bearjew11

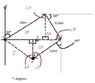
The figure shows the successive displacements of an aircraft flying a search pattern. The initial position of the aircraft is P and the final position is P'. What is the net displacement (magnitude and direction) between P and P'?


My attempt:
So, my understanding is that the net displacement of the successive displacement vectors is the overall sum of the successive displacement vectors. (?)
Also, referring to the rules of alternate interior angles, ∠A, ∠B, and ∠C = 60° (?)

ΔA
Hypotenuse = 18km
Height = 18sin60°
Base = 18cos60°

ΔB
Hypotenuse = 9.5km
Height = 9.5sin60°
Base = 9.5cos60°

ΔC
Hypotenuse = 12km
Height = 12sin60°
Base = 12cos60°

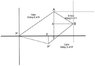
My attempt to find the base of the triangle formed by the point P and P' and the x-axis was to add the bases of ΔA and ΔB and subtract the base of ΔC from the sum.

With my calculations (using rounded decimals and plugging in the exact values):
I got ~13km for →P (incorrect because my book reads 11.2km)
and for ∠θ I got 57.1° (incorrect, because the remaining angle should be 27.7° and is 32.9° with my calculations)

I am doing something wrong. HELP

Attached Thumbnails

 

Andrew Mason

This is where you are going wrong. The displacement between P and P' is the vector going from the head of P to the head of P' (i.e. P' - P or the displacement vector that, when added to P, results in P').

AM

tms

Correct.
It's best not to think in terms of triangles, hypotenuses, bases, and heights, but to think in terms of magnitudes and directions and components.

In this particular case, you're using the wrong angle (assuming 60° is the angle between the [itex]y[/itex]-axis and the first vector).

tms

The resultant is also the sum of the three given vectors. The OP is correct on this point.

Andrew Mason

Of course you are right. I responded before the drawing was available, thinking P and P' were displacement vectors from a common origin. Sorry about the confusion.

Part of the problem here is that the diagram is misleading. The vector lengths and angles do not fit. For example, the heights of ΔA and ΔB are the same. Using the figures given, however, the height of ΔA is 18sin(30) =9 km and the height of ΔB 9.5cos(30) = 8.22 km. (In other words, arctan 9.5/18 = 27.8 deg ≠ 30 deg.).

I would suggest that you add the vector components using the angles given and disregard the triangles, as tms has suggested. The answer given is correct (11.2).

AM

tms

P and P' can be thought of as displacement vectors from the origin (or some other point); you were right on that point. But P' is also the sum of the given vectors; the OP was right about that. You were both right.

bearjew11

I see. So, since this is how I interpreted the diagram, then I was visualizing it incorrectly. You're saying, because of the angles and magnitudes given, the head of →B is not at on a point on the x-axis.

Can you elaborate on this a bit more, please?
I will upload the original diagram from my book. Maybe I will be able to better visualize it rather than using my quick sketch of the diagram drawn in MS paint.

Thanks.

tms

A vector [itex](r, \vartheta)[/itex] can be decomposed into components using [itex]x = r\;cos\; \vartheta[/itex] and [itex]y = r\; sin\; \vartheta[/itex].

Andrew Mason

Right.


The resultant sum of the two vectors (x1, y1) and (x2, y2) would be a vector (x1 + x2, y1 + y2). The angle of the resultant vector to the +x axis would be arctan((y1+y2)/(x1+x2)).

AM