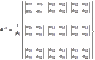Matrix has no inverse for skew symmetric matrix

[t_n_p]

[SOLVED] Show matrix has no inverse

Homework Statement

Show that for a matrix A that has dimensions n by n (where n is an odd number) and is skew symmetric (i.e. transpose of A = -A) that it has no inverse

The Attempt at a Solution

Not sure where to start but have a feeling I have to used the definition transpose of A = -A to find the determinant first.

 

[cristo]

Not sure where to start but have a feeling I have to used the definition transpose of A = -A to find the determinant first.

Good idea. If you can relate the determinant of A to the determinant of -A, then you may have a chance.

 

[t_n_p]

For starters, I've decided to choose n=3. When creating matrix A and hence -A, should I just nominate values of a,b,c etc and have the determinant in terms of each matrix entry like I've shown below? Where to from here?

http://img74.imageshack.us/img74/9438/59195012ss6.jpg

 

[cristo]

For starters, I've decided to choose n=3. When creating matrix A and hence -A, should I just nominate values of a11, a12, a13 etc and have the determinant in terms of each matrix entry?

No. You should keep n as an arbitrary odd number, and keep A an arbitrary matrix, if you want to answer the question.

Hint: How are the determinant of a matrix and its transpose related?

 

[fikus]

try to look what is
$$A^T A$$
then use the rule for determinant of product.

 

[fikus]

uhh sorry, just look what determinant of transpose matrix is as cristo said.

 

[t_n_p]

No. You should keep n as an arbitrary odd number, and keep A an arbitrary matrix, if you want to answer the question.

Hint: How are the determinant of a matrix and its transpose related?

What then?

 

[Hootenanny]

What then?

Correct. You have yet to make use if this information,

(i.e. transpose of A = -A)

 

[t_n_p]

Ok, so
|A| = |transpose of A| = |-A|

But how do I show no inverse exists?

 

[MathematicalPhysicist]

|-A|=(-1)^n|A|
but you need to know this before using this.
and there is no other way here.

 

[cristo]

|-A|=(-1)^n|A|
but you need to know this before using this.
and there is no other way here.

You should not give solutions to homework problems (and this is, in essence, a solution).

You can give hints, or suggestions of ways to attack the problem. For example, one could ask if the OP could express det(pA) in terms of det(A), in the case of an nxn matrix. The result then follows on setting p=-1. However, just giving a formula does not help the student learn anything.

 

[t_n_p]

so now
|A| = |transpose of A| = |-A| = (-1)^n|A|

I still don't get it

 

[Hootenanny]

so now
|A| = |transpose of A| = |-A| = (-1)^n|A|

Still can't see how to piece it all together though..

t_n_p, as cristo has said, you have virtually been given the answer by LQG. Try thinking about what has been said for a while before asking further questions. We won't hold you're hand through every single step of every single question, you have to do some work.

 

[t_n_p]

I've thought about it. The formula provided by LQG does not register anything to me. Yes, I know

and the determinant of A can supposedly be found using the formula provided by LQG, but my denominator thus appears merely as (-1)^n|A|. I am also unfamiliar with raising constants to the power of a matrix. I can not see how this is relevant or useful to proving the inverse does not exist. Hence my question is how is it related to what I want to know?

 

[cristo]

What is the condition for the existence of the inverse to a matrix, in terms of the determinant? This is something you learn in the first few weeks of a linear algebra course, so if you're not sure, then look through your course notes, or textbook.

 

[MathematicalPhysicist]

You should not give solutions to homework problems (and this is, in essence, a solution).

You can give hints, or suggestions of ways to attack the problem. For example, one could ask if the OP could express det(pA) in terms of det(A), in the case of an nxn matrix. The result then follows on setting p=-1. However, just giving a formula does not help the student learn anything.

yes, but from his posts here you can see that he doesn't recall this equation, this is why i urged him to prove it and then use it, if he just uses then he will not learn anything.

 

[t_n_p]

for the inverse to exist, determinant must not equal zero. So if I set the equation given by LQG and equate to zero, the inverse will not exist?

i.e. (-1)^n|A| = 0

 

[Hootenanny]

for the inverse to exist, determinant must not equal zero.

Correct. You have a further condition on the matrix which you have not yet used.

 

[cristo]

So if I set the equation given by LQG and equate to zero, the inverse will not exist?

i.e. (-1)^n|A| = 0

No, now's the time you need to think a little. Why are you setting that to zero? It seems like you're just doing it to satisfy the condition!

You know that, since the matrix is skew-symmetric, that det(A)=det(-A). You also have the expression that lqg gave you: det(-A)=(-1)^n.det(A). Put these two together, and what do you get?

I'm not sure how I can help any more without explicitly telling you the answer!

 

[t_n_p]

Ok, I think I'm looking too hard into this.

Basically I want to show that |A| = 0, and hence the inverse does not exist.

I know that
http://img142.imageshack.us/img142/876/83639370us7.jpg

Say I ignore |-A| for the time being, and therefore I have |A| = (-1)^n|A|. I then divide both sides by |A| and take log10 both sides. Am I on the right track?

 

[cristo]

What you have is det(A)=det(-A)=(-1)^n.det(A) (note that det(A) is not in the exponent!)

What do you know about n? What does the equation reduce to on utilising this condition?

 

[t_n_p]

pffft no wonder.

|A| = |-A| = (-1)^n . |A|,

since n is odd,
|A| = |-A| = -|A|

|A| = |-A| + |A|

|-A| = 0

since |-A| = |A|,

|A| = 0 and hence inverse does not exist

 

[cristo]

pffft no wonder.

|A| = (-1)^n . |A|
1 = (-1)^n

You know you can only cancel something from both sides if that thing is not zero. Here you want to show it is zero, so you can't cancel it!

Anyway, you have det(A)=-det(A). Under what conditions does this apply?

 

[t_n_p]

I've edited my above post, is your post still relevant?

Let's start from scratch.

|A| = |transpose A|

since A is skew symmetric we also know
|transpose A| = |-A|

therefore, |A| = |transpose A| = |-A|

also |-A| = (-1)^n. |A|

therefore |A| = |transpose A| = |-A|= (-1)^n. |A|

since n is odd,
|A| = |transpose A| = |-A|= (-1)|A|

 

[cristo]

I've edited my above post, is your post still relevant?

You shouldn't edit posts using the advice of the reply: it makes threads look very disjoint.

Let's start from scratch.

|A| = |transpose A|

since A is skew symmetric we also know
|transpose A| = |-A|

therefore, |A| = |transpose A| = |-A|

also |-A| = (-1)^n. |A|

therefore |A| = |transpose A| = |-A|= (-1)^n. |A|

since n is odd,
|A| = |transpose A| = |-A|= (-1)|A|

Ok, so now you're up to my last post:

Anyway, you have det(A)=-det(A). Under what conditions does this apply?

Can you answer this?

 

[t_n_p]

I've looked through my notes/textbook, can't seem to locate when |A| = -|A|. Google search says something about left handed matrix?

 

[cristo]

I've looked through my notes/textbook, can't seem to locate when |A| = -|A|. Google search says something about left handed matrix?

This is just algebra, there's nothing special to it. The determinant of a matrix is an integer, let's say d. So, you want to know for which integer does d=-d or for which integer does 2d=0?

 

[t_n_p]

when d = 0, therefore |A| = -|A| ONLY when |A| = 0

since |A| = 0, inv(A) does not exist.

SOLVED.
Thanks Cristo, appreciate it mate.

 

[cristo]

when d = 0, therefore |A| = -|A| ONLY when |A| = 0

since |A| = 0, inv(A) does not exist.

SOLVED.
Thanks Cristo, appreciate it mate.

Well done; you're welcome.