- #1
Calcotron
- 17
- 0
Prove the formula [tex] A = \frac{1}{2}r^{2}\theta[/tex] for the area of a sector of a circle with radius r and central angle [tex]\theta[/tex]. (Hint: Assume 0 < [tex]\theta[/tex] < [tex]\frac{\pi}{2}[/tex] and place the center of the circle at the origin so it has the equation [tex]x^{2} + y^{2} = r^{2}[/tex] . Then A is the sum of the area of the triangle POQ and the area of the region PQR in the figure.)
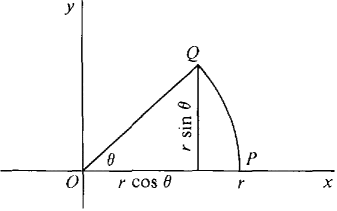
So the area of the triangle is 1/2bh which comes to [tex]\frac{1}{2}r^{2}cos\theta sin\theta[/tex]
Now, for the other region I used the integral [tex]\int\sqrt{r^{2} - x^{2}}dx[/tex]
I make x = r sin[tex]\theta[/tex]
I plug that in under the square root sign and get r cos[tex]\theta[/tex].
I changed the limits of integration from r cos[tex]\theta[/tex] to r, to pi/4 to pi/2.
Now since dx = r cos[tex]\theta[/tex]d[tex]\theta[/tex] the integral for the area of the second region is [tex]\int r^{2}cos^{2}\theta d\theta[/tex]. Now here is where the problem starts, I pull the r^2 out of the equation and use half angle theorem on the cos^2 theta. After his I end up with [tex]\frac{1}{2}r^{2}(\theta+\frac{1}{2}sin2\thetacos\theta)[/tex] with limits pi/4 to pi/2. Now I am assuming there should be a negative equivalent somewhere here to cross out the first area and leave me with just [tex]\frac{1}{2}r^{2}\theta[/tex]but I don't see how I can get it to work, especially after I finish integration and sub the limits in at which point I will lose the trig ratios. Can anyone help me finish this question up?
So the area of the triangle is 1/2bh which comes to [tex]\frac{1}{2}r^{2}cos\theta sin\theta[/tex]
Now, for the other region I used the integral [tex]\int\sqrt{r^{2} - x^{2}}dx[/tex]
I make x = r sin[tex]\theta[/tex]
I plug that in under the square root sign and get r cos[tex]\theta[/tex].
I changed the limits of integration from r cos[tex]\theta[/tex] to r, to pi/4 to pi/2.
Now since dx = r cos[tex]\theta[/tex]d[tex]\theta[/tex] the integral for the area of the second region is [tex]\int r^{2}cos^{2}\theta d\theta[/tex]. Now here is where the problem starts, I pull the r^2 out of the equation and use half angle theorem on the cos^2 theta. After his I end up with [tex]\frac{1}{2}r^{2}(\theta+\frac{1}{2}sin2\thetacos\theta)[/tex] with limits pi/4 to pi/2. Now I am assuming there should be a negative equivalent somewhere here to cross out the first area and leave me with just [tex]\frac{1}{2}r^{2}\theta[/tex]but I don't see how I can get it to work, especially after I finish integration and sub the limits in at which point I will lose the trig ratios. Can anyone help me finish this question up?
Attachments
Last edited:
