- #1
coleman123
- 17
- 0
*Edit: I noticed I may have posted this question on the wrong forum... if this is the case, could you please move it for me instead of deleting? thanks! :)
Hello, I am having problems on building my electromagnetic tensor from a four-potential. I suspect my calculations are not right. Here are the steps:
My metric is (coordinates are t,r,z,ø):
[itex]\left(
\begin{array}{cccc}
e^{2 \psi (r,z)} & 0 & 0 & 0 \\
0 & -e^{2 \gamma (r,z)-2 \psi (r,z)} & 0 & 0 \\
0 & 0 & -e^{2 \gamma (r,z)-2 \psi (r,z)} & 0 \\
0 & 0 & 0 & -e^{-2 \psi (r,z)} r^2 \\
\end{array}
\right)[/itex]
Then I have a magnetic vector potential in spherical coordinates (the coordinates are r,θ,ø):
[itex]\left\{0,0,\frac{4 \pi M \sin (\theta )}{3 r^2}\right\}[/itex]
I convert it to cylindrical coordinates r,z,ø:
[itex]\left\{0,0,\frac{4 \pi M r}{3 \left(r^2+z^2\right)^{3/2}}\right\}[/itex]
I build my contravariant four-potential (the electric potential is zero):
[itex]\left\{0,0,0,\frac{4 \pi M r}{3 \left(r^2+z^2\right)^{3/2}}\right\}[/itex]
I will use this formula to calculate the covariant electromagnetic tensor components:
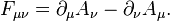 (1)
(1)
So I need the covariant four-potential, which I obtain by multiplying the contravariant four-potential by the covariant metric tensor, and performing a summation I get:
[itex]\left\{0,0,0,-\frac{4 \pi M r^3 e^{-2 \psi }}{3 \left(r^2+z^2\right)^{3/2}}\right\}[/itex]
Using (1) I calculate the covariant electromagnetic tensor, and then, raising indexes, the contravariant one is:
[itex]\left(
\begin{array}{cccc}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & \frac{4 e^{2 \psi (r,z)-2 \gamma (r,z)} M \pi \left(2 r \left(r^2+z^2\right) \psi ^{(1,0)}(r,z)-3 z^2\right)}{3 \left(r^2+z^2\right)^{5/2}} \\
0 & 0 & 0 & \frac{4 e^{2 \psi (r,z)-2 \gamma (r,z)} M \pi r \left(3 z+2 \left(r^2+z^2\right) \psi ^{(0,1)}(r,z)\right)}{3 \left(r^2+z^2\right)^{5/2}} \\
0 & -\frac{4 e^{2 \psi (r,z)-2 \gamma (r,z)} M \pi \left(2 r \left(r^2+z^2\right) \psi ^{(1,0)}(r,z)-3 z^2\right)}{3 \left(r^2+z^2\right)^{5/2}} & -\frac{4 e^{2 \psi (r,z)-2 \gamma (r,z)} M \pi r \left(3 z+2 \left(r^2+z^2\right) \psi ^{(0,1)}(r,z)\right)}{3 \left(r^2+z^2\right)^{5/2}} & 0 \\
\end{array}
\right)[/itex]
The notation above, next to my metric functions [itex]\psi[/itex] and [itex]\gamma[/itex], indicate derivatives:
(1,0) is a derivative in r
(0,1) is a derivative in z
I was not expecting my metric functions [itex]\psi[/itex] and [itex]\gamma[/itex] to appear on my contravariant electrogmagnetic tensor. I would like a help if I did all the steps right.
If I just take the curl of the magnetic vector potential to find the magnetic field, and plug in the expected components on the electromagnetic tensor, I get a different result, and was expecting the same... that is what bothers me. I'll show this now.
Calculating the magnetic field from the magnetic vector potential in cylindrical coordinates results in:
[itex]\left\{\frac{4 \pi M r z}{\left(r^2+z^2\right)^{5/2}},-\frac{4 \pi M \left(r^2-2 z^2\right)}{3 \left(r^2+z^2\right)^{5/2}},0\right\}[/itex]
I can then plug the Br and Bz components directly in the electromagnetic field tensor which is defined as (my c equals 1, and instead of x,y,z I have r,z,ø):
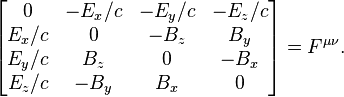
So when calculating the electromagnetic tensor this other way, I obtain a different result, without my metric functions [itex]\psi[/itex] and [itex]\gamma[/itex].
What is happening? Thanks in advance for any clarifications on this issue..
Hello, I am having problems on building my electromagnetic tensor from a four-potential. I suspect my calculations are not right. Here are the steps:
My metric is (coordinates are t,r,z,ø):
[itex]\left(
\begin{array}{cccc}
e^{2 \psi (r,z)} & 0 & 0 & 0 \\
0 & -e^{2 \gamma (r,z)-2 \psi (r,z)} & 0 & 0 \\
0 & 0 & -e^{2 \gamma (r,z)-2 \psi (r,z)} & 0 \\
0 & 0 & 0 & -e^{-2 \psi (r,z)} r^2 \\
\end{array}
\right)[/itex]
Then I have a magnetic vector potential in spherical coordinates (the coordinates are r,θ,ø):
[itex]\left\{0,0,\frac{4 \pi M \sin (\theta )}{3 r^2}\right\}[/itex]
I convert it to cylindrical coordinates r,z,ø:
[itex]\left\{0,0,\frac{4 \pi M r}{3 \left(r^2+z^2\right)^{3/2}}\right\}[/itex]
I build my contravariant four-potential (the electric potential is zero):
[itex]\left\{0,0,0,\frac{4 \pi M r}{3 \left(r^2+z^2\right)^{3/2}}\right\}[/itex]
I will use this formula to calculate the covariant electromagnetic tensor components:
So I need the covariant four-potential, which I obtain by multiplying the contravariant four-potential by the covariant metric tensor, and performing a summation I get:
[itex]\left\{0,0,0,-\frac{4 \pi M r^3 e^{-2 \psi }}{3 \left(r^2+z^2\right)^{3/2}}\right\}[/itex]
Using (1) I calculate the covariant electromagnetic tensor, and then, raising indexes, the contravariant one is:
[itex]\left(
\begin{array}{cccc}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & \frac{4 e^{2 \psi (r,z)-2 \gamma (r,z)} M \pi \left(2 r \left(r^2+z^2\right) \psi ^{(1,0)}(r,z)-3 z^2\right)}{3 \left(r^2+z^2\right)^{5/2}} \\
0 & 0 & 0 & \frac{4 e^{2 \psi (r,z)-2 \gamma (r,z)} M \pi r \left(3 z+2 \left(r^2+z^2\right) \psi ^{(0,1)}(r,z)\right)}{3 \left(r^2+z^2\right)^{5/2}} \\
0 & -\frac{4 e^{2 \psi (r,z)-2 \gamma (r,z)} M \pi \left(2 r \left(r^2+z^2\right) \psi ^{(1,0)}(r,z)-3 z^2\right)}{3 \left(r^2+z^2\right)^{5/2}} & -\frac{4 e^{2 \psi (r,z)-2 \gamma (r,z)} M \pi r \left(3 z+2 \left(r^2+z^2\right) \psi ^{(0,1)}(r,z)\right)}{3 \left(r^2+z^2\right)^{5/2}} & 0 \\
\end{array}
\right)[/itex]
The notation above, next to my metric functions [itex]\psi[/itex] and [itex]\gamma[/itex], indicate derivatives:
(1,0) is a derivative in r
(0,1) is a derivative in z
I was not expecting my metric functions [itex]\psi[/itex] and [itex]\gamma[/itex] to appear on my contravariant electrogmagnetic tensor. I would like a help if I did all the steps right.
If I just take the curl of the magnetic vector potential to find the magnetic field, and plug in the expected components on the electromagnetic tensor, I get a different result, and was expecting the same... that is what bothers me. I'll show this now.
Calculating the magnetic field from the magnetic vector potential in cylindrical coordinates results in:
[itex]\left\{\frac{4 \pi M r z}{\left(r^2+z^2\right)^{5/2}},-\frac{4 \pi M \left(r^2-2 z^2\right)}{3 \left(r^2+z^2\right)^{5/2}},0\right\}[/itex]
I can then plug the Br and Bz components directly in the electromagnetic field tensor which is defined as (my c equals 1, and instead of x,y,z I have r,z,ø):
So when calculating the electromagnetic tensor this other way, I obtain a different result, without my metric functions [itex]\psi[/itex] and [itex]\gamma[/itex].
What is happening? Thanks in advance for any clarifications on this issue..
Last edited:
