- #1
synkk
- 216
- 0
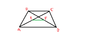
Given a trapezium ABCD with AB parallel to CD. Show that the line joining the midpoints of the diagonals is parallel to AB & CD (done). Show also that its length is the difference of AB and CD.
working:
I called the midpoint of AC, E and the midpoint of BD, F
Then found that ## \displaystyle \vec{EF} = \frac{1}{2}b + \frac{1}{2}(d-c) ## now I wasn't sure where to go from here so took a look at the solutions,
they change ## \displaystyle \vec{EF} = \frac{1}{2}b - \frac{1}{2}(c-d) ## which I understand why, however the next step baffles me
they go from:
## \displaystyle \vec{EF} = \frac{1}{2}b - \frac{1}{2}(c-d) ##
to
## \displaystyle |\vec{EF}|\hat{u} = \frac{1}{2} |\vec{AB}|\hat{u} - \frac{1}{2}|\vec{DC}|\hat{u} ##
then go on to say that the length EF is ## \frac{1}{2}(|\vec{AB}| - |\vec{DC}|) ##
what I don't understand is how the unit vector "u" got introduced, and why was it introduced? I'm not very good at maths, so please explain this in as most basic terms as possible.
I apologise for not being able to bold "a" "b" "c" "u" etc, I have no idea how to do it via latex, but they are vectors (supposed to be).
working:
I called the midpoint of AC, E and the midpoint of BD, F
Then found that ## \displaystyle \vec{EF} = \frac{1}{2}b + \frac{1}{2}(d-c) ## now I wasn't sure where to go from here so took a look at the solutions,
they change ## \displaystyle \vec{EF} = \frac{1}{2}b - \frac{1}{2}(c-d) ## which I understand why, however the next step baffles me
they go from:
## \displaystyle \vec{EF} = \frac{1}{2}b - \frac{1}{2}(c-d) ##
to
## \displaystyle |\vec{EF}|\hat{u} = \frac{1}{2} |\vec{AB}|\hat{u} - \frac{1}{2}|\vec{DC}|\hat{u} ##
then go on to say that the length EF is ## \frac{1}{2}(|\vec{AB}| - |\vec{DC}|) ##
what I don't understand is how the unit vector "u" got introduced, and why was it introduced? I'm not very good at maths, so please explain this in as most basic terms as possible.
I apologise for not being able to bold "a" "b" "c" "u" etc, I have no idea how to do it via latex, but they are vectors (supposed to be).