- #1
Jhenrique
- 685
- 4
Like we have the total differential of a function:
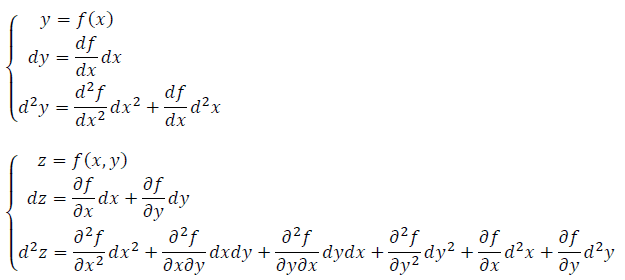
I was thinking, why not take the "total integral" of a function too? Thus I did some algebraic juggling and, how I haven't aptitude for be a Ph.D. in math, I bring my ideia for the experients from here evaluate... Anyway, the ideia is the follows:
Let y = f(x), so: [tex]\int y dx = \int f dx[/tex] [tex]\int y \frac{dx}{dx} = \int f \frac{1}{dx}dx[/tex] [tex]\int y = \int f \frac{1}{dx}dx \;\;\;\Rightarrow \;\;\; \int y du = \int f \frac{du}{dx}dx[/tex] Generalizing...
Let w = f(x,y,z), so: [tex]\int w = \int f \frac{1}{dx}dx + \int f \frac{1}{dy}dy + \int f \frac{1}{dz}dz[/tex]
I don't venture take the 2nd integral of y because I think that will arise one d²x in the denominator...
What you think about? All this make sense?
I was thinking, why not take the "total integral" of a function too? Thus I did some algebraic juggling and, how I haven't aptitude for be a Ph.D. in math, I bring my ideia for the experients from here evaluate... Anyway, the ideia is the follows:
Let y = f(x), so: [tex]\int y dx = \int f dx[/tex] [tex]\int y \frac{dx}{dx} = \int f \frac{1}{dx}dx[/tex] [tex]\int y = \int f \frac{1}{dx}dx \;\;\;\Rightarrow \;\;\; \int y du = \int f \frac{du}{dx}dx[/tex] Generalizing...
Let w = f(x,y,z), so: [tex]\int w = \int f \frac{1}{dx}dx + \int f \frac{1}{dy}dy + \int f \frac{1}{dz}dz[/tex]
I don't venture take the 2nd integral of y because I think that will arise one d²x in the denominator...
What you think about? All this make sense?