- #1
Jhenrique
- 685
- 4
What means:
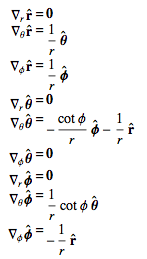
?
This guy, ##\vec{\nabla}_{\hat{\phi}} \hat{r}##, for example, means:
[tex]\\ \hat{\phi}\cdot\vec{\nabla}\hat{r} = \begin{bmatrix}
\phi _1 \\
\phi _2 \\
\end{bmatrix}
\begin{bmatrix}
\frac{\partial r_1}{\partial x} & \frac{\partial r_1}{\partial y} \\
\frac{\partial r_2}{\partial x} & \frac{\partial r_2}{\partial y} \\
\end{bmatrix}[/tex]
?
?
This guy, ##\vec{\nabla}_{\hat{\phi}} \hat{r}##, for example, means:
[tex]\\ \hat{\phi}\cdot\vec{\nabla}\hat{r} = \begin{bmatrix}
\phi _1 \\
\phi _2 \\
\end{bmatrix}
\begin{bmatrix}
\frac{\partial r_1}{\partial x} & \frac{\partial r_1}{\partial y} \\
\frac{\partial r_2}{\partial x} & \frac{\partial r_2}{\partial y} \\
\end{bmatrix}[/tex]
?