Conversion from Cartesian to toroidal coordinates

[Twinbee]

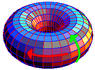
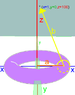
Wikipedia details the technique for converting from toroidal coords to cartesian. How do you convert the other way?

*EDIT* Is there any free (or nearly free) software which allows you to solve algebraic equations and express variables in terms of existing formulae, AND supports sin, cos, tan etc. to do so? I.e. something which would help answer my initial question.

 

[pkleinod]

phi = inverse tangent of (y/x). Let q = sqrt(x**2 + y**2). Then the bipolar coordinates can be obtained from the two foci in the xz-plane F1 (-a/2,0) and
F2 (+a/2,0) and the point P (q,z). You have the vertices of the triangle F1 P F2, so you can calculate the distances d1 and d2 and hence the coordinate tau;
the coordinate sigma can then be obtained from the law of cosines. Or have I misinterpreted the definition of the toroidal coordinates?

 

[Twinbee]

Where is q in the Wikipedia article?

I think Tau is set arbitrarily to the size of the toroid's (large) radius, so if you could also give the equations for a, and Sigma, (according to how the Wikipedia page uses them), that would be great.

 

[pkleinod]

Oh, q is simply the stuff multiplying sin(phi):
q = a sinh(tau)/(cosh (tau) -cos (sigma)), but you can see that x**2 + y**2 = q**2
because sin^2(phi) + cos^2(phi) =1. This means that q is the radius of the toroid, not tau.

 

[pkleinod]

I forgot to mention that a and sigma and tau are just as in the Wikipedia link for bipolar coordinates (one of the links on the page that you referred to). There is a nice diagram there showing the distance between the Foci (a) and the coordinates sigma and tau. NB!
That article defines sigma and tau in the xy-plane, but your equations have the bipolar coordinates in the xz-plane.

 

[Twinbee]

Thanks for your help so far!

Despite the appearance of the original question, my math isn't amazing currently, so I'm having a little difficulty comprehending the above.

If you could complete the following so as to reverse the original Wikipedia formula, that would be smashing:

phi = atan2(y,x)
Tau = anything
a = ?
Sigma = ?

I'm assuming that phi is the angle around the main large torus circle (the red arrow in the picture below), and Sigma is the angle around the smaller circle which is being 'extruded' to make the torus (the green arrow in the picture):

Click the pic to enlarge.

 

[pkleinod]

No, your interpretation of sigma is not correct. I can give you a more detailed reply later but in the meantime, go to this link:
http://en.wikipedia.org/wiki/Bipolar_coordinates
and look at the first two diagrams, relabeling the y-axis as the z-axis to agree with the toroidal coordinates that you referred to. Sigma is the angle subtended by chord of length 2a (I think I made a mistake in an earlier post: the foci lie on the x-axis at +a and -a and so are separated by 2a) at the circle of constant sigma passing through the two foci.

 

[Twinbee]

So am I thinking of Bipolar coords instead? If not, then what coordinate system am I describing?

 

[pkleinod]

Spelling it out.

Twinbee:
You are interested in toroidal coordinates in 3D, (sigma,tau,phi). These are
generated from bipolar coordinates (sigma,tau) in the 2D xz-plane by rotating
about the z-axis (i.e. in the xy-plane) by the angle phi. You want to start with some point S(x,y,z)
and you want its toroidal coordinates S(sigma,tau,phi). Do this in steps:
1) Viewing the z-axis as the polar axis, write S in terms of cylindrical
coordinates S(q,phi,z), where x = q cos(phi) and y = q sin(phi) so that
q² = x² + y² and
phi = Tan^-1(y/x).
2) This means that the point S can be obtained by rotating a point in the xz-plane,
P(q,0,z), through the angle phi about the z-axis. We
have now reduced the problem to finding the bipolar coordinates of
P(q,0,z).
3) You now have to choose the foci of the bipolar coordinates. Let the
first of these be F₁ with coordinates (-a,0,0) and the
second be F₂ at (+a,0,0). The points F₁PF₂
are the vertices of a triangle in the xz-plane.
4) the length of the line PF₁ is d₁ and that of line
PF₂ is d₂:
d₁² = (q+a)² + z²
d₂² = (q-a)² + z²
5) The coordinate tau is now obtained from its definition:
tau = log(d₁/d₂).
6) The coordinate sigma is computed from the law of cosines:
cos(sigma) = -(4a²-d₁²-d₂²)/(2d₁d₂)

That's it.
Now you should check this result. Take a point (x,y,z) and compute
(sigma,tau,phi) from the above; then, insert the result in the formula
from Wikipedia to get the original (x,y,z) back again. In this way, you
can find any mistakes I have made.

 

[Twinbee]

Heh making me jumping through hoops, or maybe I should say toruses in this case ;)
Okay, I'm getting a little bit lost. Just to make sure we understand each other, I'll paste a complete diagram I rendered in povray to show what I want:

http://www.skytopia.com/stuff/torus2.png"

("a" is the small circle radius, and may go in any direction depending on sigma)

I looked at your post above, and was maybe able to calculate tau and sigma. Can you confirm whether these match the diagram's variable names?

For step 1: For the cylindrical coords, I've now got:
S(q, phi, z) = ( sqrt(x^2+y^2) , aTan( y / x ) , z )

Not sure how that fits with the below steps though.

For step 5: tau = LogBaseE( (sqrt( (q+a)^2 + z^2) ) / (sqrt( (q-a)^2 + z^2) ) )

For step 6: sigma = acos( -( 4*a^2 - ( (q+a)^2 + z^2 ) - ( (q-a)^2 + z^2 ) ) / (2 * sqrt( (q+a)^2 + z^2) * sqrt( (q-a)^2 + z^2) ) )

(I can try and simplify step 6 later to help the speed of the program).

Problem is; what is "a" in steps 5 and 6? And do they represent the "a" as I've given in the diagram? Also I want sigma calculated efficiently from the original x,y and & z coords, but it looks as though they're going through intermediate variables (a and q), of which, "q" I calculated for the cylindrical coords. Is this correct?

Also tau can be any number, at least from what I'm defining tau as in the diagram, so why do you redefine it in step 5 instead of letting it be any number?

Just gimme phi, sigma and tau from a,x,y & z :-D :P

 

[pkleinod]

Sorry, but your diagram is completely incorrect. Please go to the link
http://en.wikipedia.org/wiki/Bipolar_coordinates
The first diagram you see displays sets of circles that intersect at right angles. The ones that pass through the two foci are curves of constant sigma, the others are curves of constant tau. Note that you should relabel the Y-axis as the z-axis in order to agree with the equations in the Wikipedia article that you referred to. The second diagram shows a red circle passing through the two foci (F1 at (-a,0) and F2 at (a,0)) and the point P(q,0,z). Sigma is clearly marked here. It is the angle subtended by the chord F1F2 at any point on the circle. The distances d1 and d2 from the point P to each of the foci are also shown. tau is log(d1/d2) BY DEFINITION. (Note that tau is not any old number but is determined from x,y,z and the position of the foci.) The point (x,y,z) is obtained by rotating the point P through an angle phi about the z-axis (i.e. in the plane Z=z). So, once you have chosen the parameter "a" to fit your problem, then the toroidal coordinates of any point (x,y,z) may be obtained from the program:

phi = ATAN2(y/x)
q = SQRT(x**2 + y**2)
d1 = SQRT((q+a)**2 + z**2)
d2 = SQRT((q-a)**2 + z**2)
tau = LOG(d1/d2)
sigma = ACOS( (d1**2 + d2**2 - 4*a**2)/(2*d1*d2) )

If you wish to improve on the efficiency of this program, be my guest. There are many ways to skin a cat.

 

[Twinbee]

I had a look at the Bipolar link earlier but couldn't make much sense of it at the time. Like I said before, my math isn't amazing. I'll try again.

For now, when you say the diagram is incorrect, do you mean the names given to each variable (tau, phi etc. are mixed up), or the coordinate system itself I am attempting to use aswell?

To be honest, they can be called anything - just a, b, c, d if you like. All I need to know is how to convert them to x, y and z, and back.

That is of course that my coordinate system in the diagram makes sense, which perhaps you can confirm (ignoring the variables names which can be anything). To me, it really seems to be the most intuitive and simplest way of creating a "toroidal coord system", but maybe there's a couple of other ways too.

Thanks for the formulae at the end. I'm guessing this produces a different coord system to the one I'm thinking, but I'll try it out anyway...

 

[pkleinod]

No, it has nothing to do with the labels or their names. I am afraid your whole conception about the way the coordinate system looks like is mistaken. Your diagram looks like a ring of baloney (which is a torus, granted) that is sliced
through. Your angle sigma seems to be associated with just one end of the sliced-through torus, whereas sigma is supposed to have something to do with both of the circles of the sliced-through torus. Actually, the picture in 3D of these coordinates is more complicated than a torus. In the first picture of the bipolar diagram, consider just one of the circles through the foci (i.e. the circle of constant sigma) and one of the circles of constant tau about a focal point. Now grab the vertical axis between your thumb and index finger and twirl it about the vertical axis as you would spin a top. The circle through the foci will then sweep out a sphere in 3D, while the other circle will sweep out a torus around the vertical axis. Do you see that?

Your original post referred to a set of equations relating Cartesian coordinates to toroidal coordinates. These equations define everything and they are all I have to go on! There is no room for "intuition" anymore. Now if you wish to define some other kind of coordinates, that is up to you. You are free to do what you wish but then you have to tell me what they are!

It may be none of my business but what do you want these coordinates for? Do you have some problem or project where the "ring of baloney" would seem
appropriate? Then it may well be that you in fact need some coordinates other than the ones described by the equations in your original post! Mull it over.

 

[Twinbee]

Your diagram looks like a ring of baloney (which is a torus, granted) that is sliced
through.

I'm sure you know this, but the 'half-eaten' effect was just for illustration purposes to clarify.

Your angle sigma seems to be associated with just one end of the sliced-through torus

Not sure if this is clear in the diagram, but the sigma rotation can be at any position around the large circle too (phi in my diagram).

I was going to mull everything over, but just before I do, I found this website just tonight. Inside (top left of page), I found a *very* similar diagram to my own, which is kinda weird, because I 'came up' with what I thought were toroidal coords, and this site seems to have the same system I found. Admittedly, it doesn't explicitly say "toroidal coords", but at least it shows that the system is usable and logical as a coord system. Heck, they may even be toroidal coords for all I know...

 

[Twinbee]

Okay, I've had time to return to this to think about it a little more. For your interest, all of this is intended in the hope of creating interesting 3D fractals with detail in all 3 dimensions, rather than 1 or 2 that "quaternion" fractals usually have.

The system I 'wanted' is indeed described on that page I mentioned using:

x = (a – b*cos(B)) * cos(A)
y = (a – b*cos(B)) * sin(A)
z = b*sin(B)

What coordinate system is this? So basically, I want to retrieve a,b,A,B from using x y z. Any idea how?

I've looked at the Wikipedia page again, and I think you updated it - nice one! I'll try and explain the 'proper' toroidal coord system, and you can see if I understand it soon...

 

[pkleinod]

... For your interest, all of this is intended in the hope of creating interesting 3D fractals with detail in all 3 dimensions, rather than 1 or 2 that "quaternion" fractals usually have.

OK, now I know what you are aiming for, but what role does the torus play in this?

x = (a – b*cos(B)) * cos(A)
y = (a – b*cos(B)) * sin(A)
z = b*sin(B)

What coordinate system is this? So basically, I want to retrieve a,b,A,B from using x y z. Any idea how?

I assume that (x,y,z) are the Cartesian coordinates. a and b are the major and minor radii of the torus, respectively; A is the angle for the rotation in the xy-plane; B is the angle for a rotation in the xz-plane. These equations tell you the Cartesian coordinates (x,y,z) of any point on the torus with fixed parameters a and b and the two coordinates A and B.
This is not a relation between two coordinate systems. Why? Because the (x,y,z) can describe any point in 3D space, whereas A and B describe only those points
on the surface of a particular torus characterised by a and b.

How are you going to specify four things (a,b,A,B) given only three coordinates (x,y,z)? Suppose you choose some value for b. Then, from z you might be able to calculate B = arcsin(z/b). Then you might be able to get a from
(x² + y²). Finally A=arctan(y/x). But this will be to no avail because a and B will depend upon the value that you chose for b; i.e. your "coordinate system" transformation is not unique.

In summary: either you wish to express points on the surface of a particular torus in terms of Cartesian coordinates, in which case you can only go one way (a,b,A,B ---> x,y,z) OR
you wish to express all points in 3D in terms of several different coordinate systems that can do this (e.g. the toroidal coordinates of the OP), in which case it is usually possible to obtain one set of coordinates from the other.

I've looked at the Wikipedia page again, and I think you updated it - nice one!

"Not I", said the cat. Life is too short to keep up with Wikipedia.

 

[Twinbee]

As far as I know, it is possible to express all points in space through 'my' system, because you can set "b" to be as arbitrarily large as you need. You're right the system isn't unique because the large radius (the variable "a") can be any amount, but let's stick with a=1.0 for now.

By the way, I'm also aware that there could be more than one way of representating the same XYZ point in my coords (as b gets larger, the torus coord may come through the center and out the other side), but this is fine also - we just pick the one that doesn't go 'through the center' like this.

Have you ever seen Romanesco Broccoli? You'll find that there's a distinct lack of fractals that have that kind of amazing detail in 3D. I hope to use these pseudo-toroidal coords and the basic mandelbrot fractal to realize a fantastic 3D Mandel-bulb shape, or something else a bit like it. I'll probably fail, but what the heck - it's fun trying.

 

[pkleinod]

As far as I know, it is possible to express all points in space through 'my' system, because you can set "b" to be as arbitrarily large as you need...but let's stick with a=1.0 for now.

OK. How about the point (1,0,100)? Remember that b must not be greater
than "a" in a torus.

No, I haven't seen the broccoli stuff before. Nice. There is a publication about
3D fractals: Lasenby, J, R. Lasenby, A. Lasenby, and R. Wareham. "Higher
dimensional fractals in geometric algebra."
Technical Report CUED/F-INFENG/TR.556, Cambridge University
Engineering Department, 2006. Might be interesting for you.

 

[Twinbee]

OK. How about the point (1,0,100)? Remember that b must not be greater
than "a" in a torus.

(Okay I'm assuming here that x=1, y=0, z=100 where the z axis is going up and down the center hole of the torus (see diagram).

The thing is; b can be greater than a as long as it does not cross the centre of the torus. Look in the diagram, the yellow line (b) is greater than "a". I know this would make the underlying torus shape look strange (very bloated, and overlapping itself etc.), but that's fine - the topology is still intact.

Hope you like the diagram again. I do my utmost to make it as clear as poss, even by making the y line look as though it's going off into the distance :)

Thanks for the fractal reference btw - I'll look out for it. I doubt anyone's found any truly 3D fractal which doesn't merely exhibit mostly self-similar detail though (unlike the mandelbrot, which is pseudo self-similar, allowing far greater variety).

 

[Twinbee]

Is this a tricky one to solve? I suspect so...

 

[pkleinod]

Sorry, I thought we were done. No, it's not tricky at all:
a, x, y, and z are known. Let u = a - $$\sqrt(x^2 + y^2)$$. Then

$$b = \sqrt(u^2 + z^2)$$

$$B = \sin^{-1}(z/b)$$

$$A = \tan^{-1}(y/x)$$.

Good luck with this transformation. I wouldn't touch it with a barge pole. Don't know why, just a feeling in my bones. Maybe it's OK but it might be tricky to apply.

 

[Twinbee]

Good luck with this transformation. I wouldn't touch it with a barge pole. Don't know why, just a feeling in my bones. Maybe it's OK but it might be tricky to apply.

Heh mathematician's intuition eh? :) I kinda see what you mean, but the formulae is relatively simple, and the 'overlapping' aspect can be avoided in practise if need be. Either way, I'll let you know if I ever get anything interesting from this!

Just to tie this up with a few notes. Your formulae works a dream, but also requires just a couple of IF statements to work 100% (atan2 is of no use here interestingly)...

if (x*x + y*y > 1.0) THEN B = 180 - B;
if (x<0) THEN A += 180.0;

(At least I think that's right from the tests I've done)

By the way, the reason I thought you edited the Wikipedia article is because the "Inverse transformation" is so similar to yours here on the first page, but that could be cooincidence. There is one difference however. You have:
sigma = ACOS( (d1**2 + d2**2 - 4*a**2)/(2*d1*d2) )

...while the Wikipedia articles uses the equivalent of:
sigma = ACOS( (-d1**2 - d2**2 + 4*a**2)/(2*d1*d2) )

Perhaps you could confirm which is correct.

Many thanks again for all your trouble. Dunno how you solved it (algebraically, or otherwise?). If you have a Paypal email, I'll send you some cash.

 

[pkleinod]

By the way, the reason I thought you edited the Wikipedia article is because the "Inverse transformation" is so similar to yours here on the first page, but that could be cooincidence. There is one difference however. You have:
sigma = ACOS( (d1**2 + d2**2 - 4*a**2)/(2*d1*d2) )

...while the Wikipedia articles uses the equivalent of:
sigma = ACOS( (-d1**2 - d2**2 + 4*a**2)/(2*d1*d2) )

Perhaps you could confirm which is correct.

Let a, b and c be vectors defining a triangle:

a + b + c = 0

Move c to the right-hand-side and square:

(a + b)(a + b) = c²

Use the fact that the square of a vector (x) is equal to its magnitude (X) squared
to get

A² + B² + (ab + ba) = C²
2 a.b = 2AB cos(a,b) = C² -A² - B².

(a,b) is the angle between the vectors a and b, i.e. it is the angle exterior to the triangle.
If you want the supplement of this angle, just change the sign of the rhs of the last equation.

In the Wikipedia article, the angle sigma is the interior angle,
so the sign on the rhs of the above formula should
be changed. This means that the formula given in Wikipedia is incorrect.

Many thanks again for all your trouble. Dunno how you solved it (algebraically, or otherwise?). If you have a Paypal email, I'll send you some cash.

Your "many thanks" is payment enough. Send the money to the red cross or
something similar.