- #1
bobred
- 173
- 0
Homework Statement
I am asked to write down the equation of motion of [tex]m[/tex] with respect to O, hence show that [tex]x(t)[/tex] satisfies the differential equation.
[tex]m\ddot{x}+r\dot{x}+kx=mg+kl_0+m\ddot{y}[/tex]
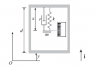
See attached diagram.
Homework Equations
I have the force of the spring H, the Damping R and the weight W as
[tex]\bold{H}=k(x-y-l_0)\bold{i}[/tex]
[tex]\bold{R}=r\dot{x}\bold{i}[/tex]
[tex]\bold{W}=-mg\bold{i}[/tex]
The Attempt at a Solution
Using the above forces and [tex]\bold{F}=m\ddot{x}[/tex], what I get is
[tex]m\ddot{x}-r\dot{x}-kx=-mg-kl_0-ky[/tex]
Do I have the forces H, R and W correct, if so how how do I get
[tex]m\ddot{x}+r\dot{x}+kx=mg+kl_0+m\ddot{y}[/tex] ?
Thanks, James
Attachments
Last edited:
 ]
] ). I'm fairly confident now my advice should much better in this post.]
). I'm fairly confident now my advice should much better in this post.]