- #1
HIUk
- 2
- 0
Hi,
I have tried to understand powder diffraction "spectrum". What I do understand is that those diffraction peaks are peaks from ewalds sphere. What I don't understand is how one can get planes and (3d) base vectors out of that. I would really appreciate some help?
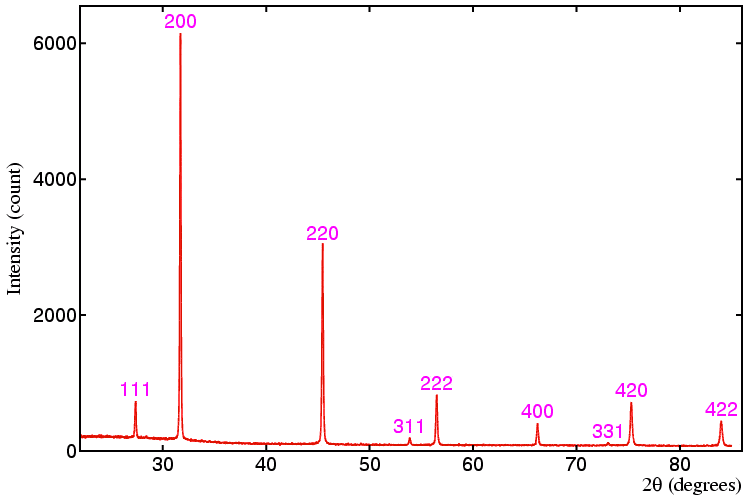
I have tried to understand powder diffraction "spectrum". What I do understand is that those diffraction peaks are peaks from ewalds sphere. What I don't understand is how one can get planes and (3d) base vectors out of that. I would really appreciate some help?