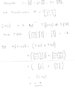- #1
Philip Wood
Gold Member
- 1,220
- 78
This is perhaps more a maths question, but it's about a piece of maths that physicists use a lot, and I'm interested in physicists' views. The question is, perhaps, rather subtle (though I hope not pedantic), and will take a bit of explaining. Sorry.
We're told that magnetic flux density and angular momentum are pseudovectors. Home in on flux density, B. Suppose we have a current-carrying loop, and another current carrying loop, which is a reflection in a plane of the first one. In each case the B (say at the centre of the loop) is related to the sense of the current by a right hand rule. This means that if the coil's plane is parallel to the reflection plane, then the B produced by the loops is normal to the reflecting plane and in the same direction - not opposite directions. An ordinary vector normal to the reflecting plane would be reversed by the reflecting plane. Conversely, the field due to a loop with its plane normal to the reflecting plane would produce a B parallel to the plane, but the B due to the reflected loop would be antiparallel to the first B. An ordinary vector parallel to the reflecting plane would not be reversed by the reflecting plane. There's a nice diagram in wiki under pseudovector - an excellent article in anycase.
Now the direction of B due to a square loop is that of c = axb in which a and b are are vectors representing successive adjacent sides directed according to the current.
The reflection behaviour is captured by the equation
R(axb) = -R(a)xR(b).
R is the operation of reflection in the plane. In words, the reflected cross product (vector product) of a and b is in the opposite direction to the cross product of the reflection of a and the reflection of b.
Now here's my question... Why is this behaviour regarded as a feature of the 'output vector', c, of the cross-product operation, rather than as a feature of the operation itself? It seems to me that c calculated for the unreflected system is just a vector, which reflects (see left hand side of equation above) as a normal (polar) vector reflects.
R(a)xR(b) is surely not sensibly regarded as the transformation (by reflection) of axb, since it has different vector 'inputs': R(a) and R(b) rather than a and b. [It's a bit like claiming that when we produce a real number c from the operation axb=c, then c isn't an ordinary real number because if we multiply it by -1 we get a different result from when we input -a and -b, instead of a and b, into axb=c.]
To sum up: why do we speak of pseudovectors and vectors rather than simply drawing attention to the reflection quirk of the vector product operation, as summed up in the equation above? [Or, to return to the current loop, why do we speak of B not obeying the same reflection rules as an ordinary vector, when we're not actually comparing B's due to the same current loop, but B's due to a current loop and its reflection?]
We're told that magnetic flux density and angular momentum are pseudovectors. Home in on flux density, B. Suppose we have a current-carrying loop, and another current carrying loop, which is a reflection in a plane of the first one. In each case the B (say at the centre of the loop) is related to the sense of the current by a right hand rule. This means that if the coil's plane is parallel to the reflection plane, then the B produced by the loops is normal to the reflecting plane and in the same direction - not opposite directions. An ordinary vector normal to the reflecting plane would be reversed by the reflecting plane. Conversely, the field due to a loop with its plane normal to the reflecting plane would produce a B parallel to the plane, but the B due to the reflected loop would be antiparallel to the first B. An ordinary vector parallel to the reflecting plane would not be reversed by the reflecting plane. There's a nice diagram in wiki under pseudovector - an excellent article in anycase.
Now the direction of B due to a square loop is that of c = axb in which a and b are are vectors representing successive adjacent sides directed according to the current.
The reflection behaviour is captured by the equation
R(axb) = -R(a)xR(b).
R is the operation of reflection in the plane. In words, the reflected cross product (vector product) of a and b is in the opposite direction to the cross product of the reflection of a and the reflection of b.
Now here's my question... Why is this behaviour regarded as a feature of the 'output vector', c, of the cross-product operation, rather than as a feature of the operation itself? It seems to me that c calculated for the unreflected system is just a vector, which reflects (see left hand side of equation above) as a normal (polar) vector reflects.
R(a)xR(b) is surely not sensibly regarded as the transformation (by reflection) of axb, since it has different vector 'inputs': R(a) and R(b) rather than a and b. [It's a bit like claiming that when we produce a real number c from the operation axb=c, then c isn't an ordinary real number because if we multiply it by -1 we get a different result from when we input -a and -b, instead of a and b, into axb=c.]
To sum up: why do we speak of pseudovectors and vectors rather than simply drawing attention to the reflection quirk of the vector product operation, as summed up in the equation above? [Or, to return to the current loop, why do we speak of B not obeying the same reflection rules as an ordinary vector, when we're not actually comparing B's due to the same current loop, but B's due to a current loop and its reflection?]
Last edited: