- #1
TrifidBlue
- 16
- 0
I hope this the right place to post my question...
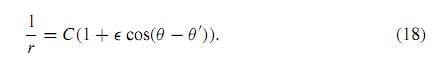
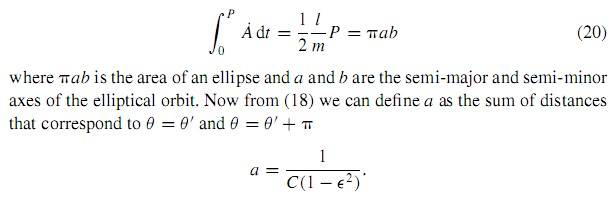
should it be, "we can define a as half the sum of distances..."?
please correct and explain if I'm mistaken
thanks
should it be, "we can define a as half the sum of distances..."?
please correct and explain if I'm mistaken
thanks
Last edited: