- #1
kelvin490
Gold Member
- 228
- 3
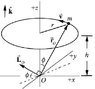
Suppose there is a point mass performing circular motion about an axis shown below:
https://drive.google.com/file/d/0B36r-g6bshskV2hIcl91aXl4ZzA/edit?usp=sharing
If the angular momentum is taken about the origin O, then the angular momentum L is not parallel to the axis of rotation. As the mass is moving in the circular orbit a torque is needed because L is keep on changing direction.
However, if the angular momentum is taken about the center of circular motion, then L is always parallel to the axis of rotation and no torque is needed to maintain the circular motion.
How to solve this paradox?
https://drive.google.com/file/d/0B36r-g6bshskV2hIcl91aXl4ZzA/edit?usp=sharing
If the angular momentum is taken about the origin O, then the angular momentum L is not parallel to the axis of rotation. As the mass is moving in the circular orbit a torque is needed because L is keep on changing direction.
However, if the angular momentum is taken about the center of circular motion, then L is always parallel to the axis of rotation and no torque is needed to maintain the circular motion.
How to solve this paradox?
Attachments
Last edited by a moderator: