- #1
Telemachus
- 835
- 30
Hi there. I have the next exercice: Verify the Green theorem with the field [tex]F(x,y)=(x+y,2x-y)[/tex], and the path which its image is the boundary positively oriented for the region between [tex]x^2+y^2=9[/tex] y [tex]|x|+|y|=1[/tex]
At first I've drawn this:
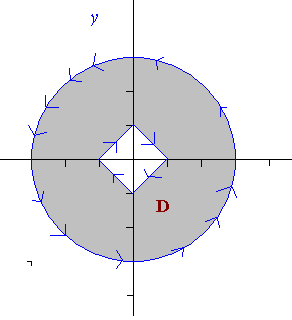
Then I've parametrized the path
[tex]\lambda_1[0,2\pi]\rightarrow{\mathbb{R}^2}:\lambda_1(t)=(3\cos t,3\sin t)[/tex]
[tex]\lambda_2[-1,1]\rightarrow{\mathbb{R}^2}:\lambda_2(t)=(t,1-|t|)[/tex]
[tex]\lambda_3[1,-1]\rightarrow{\mathbb{R}^2}:\lambda_3(t)=(t,|t|-1)[/tex]
[tex]\lambda=\lambda_1+\lambda_2+\lambda_3[/tex]
[tex]I_1=\displaystyle\int_{0}^{2\pi}(-(3\cos t+3 \sin t)3\sin t+(6\cos t-3\sin t)3\cos t)dt=9\pi[/tex]
[tex]I_2=\displaystyle\int_{-1}^{1}[t+1-|t|+(2t-1+|t|)sg(t)]dt=3[/tex]
[tex]I_2=\displaystyle\int_{1}^{-1}[t+|t|-1+(2t-|t|+1)sg(t)]dt=-1[/tex]
[tex]\displaystyle\int_{\lambda}^{}F\cdot{d\lambda}=I_1+I_2+I_3=9\pi+2[/tex]
Then I made the double integral:
[tex]\displaystyle\int \int_{D} \left ( \frac{{\partial Q}}{{\partial x}}-\frac{{\partial P}}{{\partial y}} \right )dxdy[/tex]
[tex]\displaystyle\int_{-3}^{3}\displaystyle\int_{-\sqrt[ ]{9-x^2}}^{\sqrt[ ]{9-x^2}}dydx-\displaystyle\int_{-1}^{1}\displaystyle\int_{|x|-1}^{1-|x|}dydx=\displaystyle\int_{0}^{r} \int_{0}^{2\pi}r d \theta dr - \displaystyle\int_{-1}^{1}\displaystyle\int_{-1}^{1}\displaystyle\frac{1}{2}dvdu=9\pi-2[/tex]
In the last integral I've made the change of variables [tex]y+x=u,y-x=v[/tex]. As you can see I have a problem with a sign, in the 2. Perhaps I should take the opposite signs because lambda2 and lambda3 are "negative" oriented? I thought the sign should came naturally given by the parametrization, so I'm not sure what I did wrong here.
Bye and thanks :)
At first I've drawn this:
Then I've parametrized the path
[tex]\lambda_1[0,2\pi]\rightarrow{\mathbb{R}^2}:\lambda_1(t)=(3\cos t,3\sin t)[/tex]
[tex]\lambda_2[-1,1]\rightarrow{\mathbb{R}^2}:\lambda_2(t)=(t,1-|t|)[/tex]
[tex]\lambda_3[1,-1]\rightarrow{\mathbb{R}^2}:\lambda_3(t)=(t,|t|-1)[/tex]
[tex]\lambda=\lambda_1+\lambda_2+\lambda_3[/tex]
[tex]I_1=\displaystyle\int_{0}^{2\pi}(-(3\cos t+3 \sin t)3\sin t+(6\cos t-3\sin t)3\cos t)dt=9\pi[/tex]
[tex]I_2=\displaystyle\int_{-1}^{1}[t+1-|t|+(2t-1+|t|)sg(t)]dt=3[/tex]
[tex]I_2=\displaystyle\int_{1}^{-1}[t+|t|-1+(2t-|t|+1)sg(t)]dt=-1[/tex]
[tex]\displaystyle\int_{\lambda}^{}F\cdot{d\lambda}=I_1+I_2+I_3=9\pi+2[/tex]
Then I made the double integral:
[tex]\displaystyle\int \int_{D} \left ( \frac{{\partial Q}}{{\partial x}}-\frac{{\partial P}}{{\partial y}} \right )dxdy[/tex]
[tex]\displaystyle\int_{-3}^{3}\displaystyle\int_{-\sqrt[ ]{9-x^2}}^{\sqrt[ ]{9-x^2}}dydx-\displaystyle\int_{-1}^{1}\displaystyle\int_{|x|-1}^{1-|x|}dydx=\displaystyle\int_{0}^{r} \int_{0}^{2\pi}r d \theta dr - \displaystyle\int_{-1}^{1}\displaystyle\int_{-1}^{1}\displaystyle\frac{1}{2}dvdu=9\pi-2[/tex]
In the last integral I've made the change of variables [tex]y+x=u,y-x=v[/tex]. As you can see I have a problem with a sign, in the 2. Perhaps I should take the opposite signs because lambda2 and lambda3 are "negative" oriented? I thought the sign should came naturally given by the parametrization, so I'm not sure what I did wrong here.
Bye and thanks :)