- #1
aaaa202
- 1,169
- 2
There is no net torque in this system so angular momentum should be conserved. I can't see how that is however.
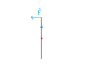
Our system is: A stick with a massless spring attached at one end. The spring is compressed and at the other end there is a point particle of mass m.
The spring is then released. Causing a torque on the particle as well as on the stick relative to the center of mass of the stick, the torquevectors being of same length but opposite sign. The pole will rotate and its angular momentum will remain the same (right?). But the particle will move away from the pole and thus change its location relative to the center of mass of the stick. But does that then not mean that the angular momentum will change? Or is it wrong to use the center of mass of the stick?
Our system is: A stick with a massless spring attached at one end. The spring is compressed and at the other end there is a point particle of mass m.
The spring is then released. Causing a torque on the particle as well as on the stick relative to the center of mass of the stick, the torquevectors being of same length but opposite sign. The pole will rotate and its angular momentum will remain the same (right?). But the particle will move away from the pole and thus change its location relative to the center of mass of the stick. But does that then not mean that the angular momentum will change? Or is it wrong to use the center of mass of the stick?