- #1
ainster31
- 158
- 1
Why is the math in the red box necessary? According to this definition, it isn't:
Proving a set of functions is orthogonal
- Thread starter ainster31
- Start date
-
- Tags
- Functions Orthogonal Set
In summary, the math in the red box is necessary to prove that a set of real-valued functions is orthogonal according to definition 12.1.3. It is specifically necessary to prove (φ0, φn) = 0, even though it is already contained as a particular case for arbitrary m and n. The proof can be simplified by using cos a = Re (e^ia).
Why is the math in the red box necessary? According to this definition, it isn't:
- #2
tiny-tim
Science Advisor
Homework Helper
- 25,839
- 258
hi ainster31! 
sorry, i don't understand your question
…
the red box proves that (φ0, φn) = 0 (for n ≠ 0)
ainster31 said:Why is the math in the red box necessary? According to this definition, it isn't:
sorry, i don't understand your question
…the red box proves that (φ0, φn) = 0 (for n ≠ 0)
- #3
ainster31
- 158
- 1
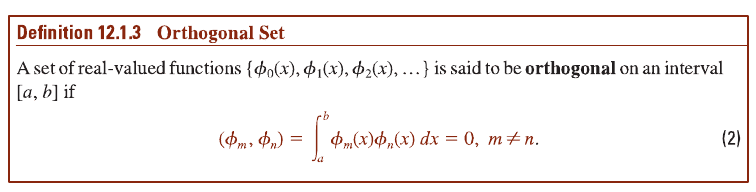
tiny-tim said:hi ainster31!
sorry, i don't understand your question
the red box proves that (φ0, φn) = 0 (for n ≠ 0)
According to definition 12.1.3, a set of real-valued functions can be proven to be orthogonal if (φm, φn) = 0. So why is it necessary to prove (φ0, φn) = 0?
- #4
- 13,349
- 3,122
m=0 is contained as a particular case for arbitrary m and n. It's no need to make the particular case. The proof goes directly by putting cos a = Re (e^ia).
- #5
ainster31
- 158
- 1
dextercioby said:
So you're saying it was unnecessary?
dextercioby said:
That went over my head.
- #6
tiny-tim
Science Advisor
Homework Helper
- 25,839
- 258
ainster31 said:
because φo is a member of the set
- #7
- 13,349
- 3,122
ainster31 said:
That's exactly what I meant.
What does it mean for a set of functions to be orthogonal?
Orthogonality refers to the mathematical concept of two or more objects being perpendicular or at right angles to each other. In the context of functions, orthogonality means that the inner product (or dot product) of any two functions in the set is equal to zero.
Why is proving a set of functions is orthogonal important?
Proving that a set of functions is orthogonal is important because it allows us to determine if the functions are linearly independent. This is a crucial concept in many areas of mathematics, such as in solving differential equations, Fourier analysis, and linear algebra.
What is the process for proving a set of functions is orthogonal?
The process for proving a set of functions is orthogonal involves using the definition of orthogonality and the properties of inner products to show that the inner product of any two functions in the set is equal to zero. This typically involves using integration techniques and algebraic manipulations.
What are some common techniques used in proving a set of functions is orthogonal?
Some common techniques used in proving a set of functions is orthogonal include the use of trigonometric identities, substitution, integration by parts, and using known orthogonal functions (such as the Legendre polynomials or the trigonometric functions) to help simplify the inner product.
Can a set of functions be proven to be orthogonal without using integration?
Yes, it is possible to prove that a set of functions is orthogonal without using integration. This can be done by using the definition of orthogonality and properties of inner products, along with algebraic manipulations, to show that the inner product of any two functions in the set is equal to zero. However, integration is often a useful tool in proving orthogonality and may make the process easier.
Similar threads
-
Differential Equations
-
Calculus and Beyond Homework Help
-
Linear and Abstract Algebra
-
Differential Equations
-
Differential Equations
-
Differential Equations
-
Differential Equations