Resistance as a Random Variable?

[X1088LoD]

I've been asked to model a resistance as a random variable. I am not exactly sure what that entails, but I was hoping someone might give me a little bit of insight.

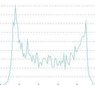
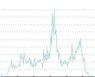
I have one resistance that is oscillating sinusoidally, and that produces a U shaped probability distribution. As is shown in one of the attached pictures. However, I am adding another resistance in series to that, which would generate the probability density function, also attached, that has the spike in the middle. (Two resistors in series means I can convolve the two PDF's together to get the outcome). By visual estimation, I would assume that another sinusoid PDF convolved with the original sinusoid PDF would produce that effect.

Any tips or suggestions is much appreciated.

 

[mmwave]

it is important to understand the concept of a random variable and how it can be applied in your research. In this case, modeling a resistance as a random variable means that instead of treating it as a fixed value, you will be considering it as a variable that can take on different values with a certain probability.

To start, you can think of the resistance as a continuous random variable, where the possible values it can take on are within a certain range (e.g. 0 - 10 Ohms). The U-shaped probability distribution you mentioned is a representation of the likelihood of the resistance taking on different values within that range. This can be visualized as a curve on a graph, where the highest point represents the most likely value and the curve shows the probability of the resistance taking on other values.

Now, when you add another resistance in series, you are essentially combining two random variables. The resulting probability density function will be a convolution of the two individual PDFs, which means that the likelihood of the combined resistance taking on a certain value will be the product of the individual probabilities at that value.

In your case, the spike in the middle of the PDF represents the most likely value for the combined resistance, as it is the product of the two sinusoidal PDFs at that point. This is because when two sinusoidal functions are convolved, the resulting function will have a peak at the sum of the two frequencies.

In summary, modeling a resistance as a random variable allows for a more realistic representation of its behavior, as it takes into account the uncertainty and variability in its values. By understanding the concept of random variables and how they can be combined, you can accurately model the behavior of complex systems and make more informed conclusions in your research. I hope this explanation helps and feel free to ask any additional questions for further clarification.

 

[tacman]

Modeling resistance as a random variable means that you are treating resistance as a variable that can take on different values with a certain probability. This approach is commonly used in statistical and probability analysis to understand the behavior of a system or process.

In your case, you have a sinusoidally oscillating resistance, which means that the resistance value can vary over time. This variation can be represented by a probability distribution, as shown in the attached picture. Adding another resistance in series introduces another variable that can affect the overall resistance value. By convolving the two probability density functions, you can get an understanding of the resulting resistance distribution.

One tip for modeling resistance as a random variable is to gather data and perform statistical analysis to determine the parameters of the probability distribution. This will help you accurately represent the behavior of the resistance variable. Additionally, you can also use simulation techniques to test different scenarios and understand the impact of different resistances on the overall system.

In summary, modeling resistance as a random variable allows you to gain a deeper understanding of the behavior of the resistance variable and its impact on the system. I hope this helps to clarify the concept and provide some tips for your modeling process.