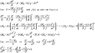- #1
Rruffpaw
- 4
- 0
The equation of motion of a rocket with mass depletion during ascent and subject to drag forces can be written as
M(t) dV/dt = A - M(t)g - BV^2 (Eq. 1)
with initial condition V(t=0) = 0 (V is velocity and t is time)
Let us assume a linear mass depletion according to
M(t) = Mo - Kt (Eq. 2)
In Eqs 1 and 2, A, B, g, Mo and K are all constants >/= 0
For the limiting case B = 0, Eq. 1 reduces to a nicely separable form and can easily be solved. For B =/= 0, Eq. 1 can be cast as
dV/dt + p(t)V^2 = q(t) (Eq. 3)
where
p(t) = B/(M(t)
and
q(t) = A/M(t) - g
However, the non-linearity (in V) of Eq. 3 leaves me stuck, since the traditional Variation of Parameters approach does not apply.
Any ideas on how to proceed (in the context of an analytical or at least a semi-analytical solution) would be deeply appreciated.
-Sharat
M(t) dV/dt = A - M(t)g - BV^2 (Eq. 1)
with initial condition V(t=0) = 0 (V is velocity and t is time)
Let us assume a linear mass depletion according to
M(t) = Mo - Kt (Eq. 2)
In Eqs 1 and 2, A, B, g, Mo and K are all constants >/= 0
For the limiting case B = 0, Eq. 1 reduces to a nicely separable form and can easily be solved. For B =/= 0, Eq. 1 can be cast as
dV/dt + p(t)V^2 = q(t) (Eq. 3)
where
p(t) = B/(M(t)
and
q(t) = A/M(t) - g
However, the non-linearity (in V) of Eq. 3 leaves me stuck, since the traditional Variation of Parameters approach does not apply.
Any ideas on how to proceed (in the context of an analytical or at least a semi-analytical solution) would be deeply appreciated.
-Sharat