Two oscillating masses on springs in one dimension

[99wattr89]

I can't make this question work, so I'm hoping that someone here will be able to help guide me towards a solution.

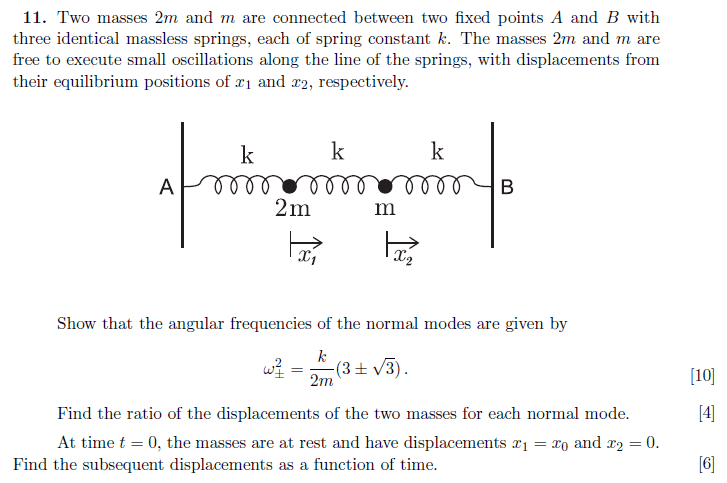
I began with F=ma, and wrote down the equations of motion for each of the masses.

a) 2mx^..₁ = -kx₁ -k(x₁ -x₂)

and

b) mx^..₂ = -kx₂ +k(x₁ -x₂)Then I added b to a, and subtracted b from a to get;

c) m(2x^..₁ +x^..₂) = -k(x₁ +x₂)

and

d) m(2x^..₁ -x^..₂) = -3k(x₁ -x₂)Then I added d to c, and subtracted d from c to get;

e) mx^..₁ = -kx₁

and

f) mx^..₂ = kx₁ -2kx₂I then tried to solve e, using the trial solution x₁ = αcosωt + βsinωt
But I don't have boundary conditions, so I can't find α and β, just ω, which I found to be √(k/m)I then tried putting this expression into f to allow me to solve it for x₂, but I realized that I could only solve it if the ω term associated with x₁ was the same as the ω term associated with x₂ - otherwise the sin and cos terms can't be canceled out. And if ω is the same for both then my method has to be wrong anyway, because I'm meant to find two values for ω, and as the question states, neither is √(k/m)Can anyone help me here?

Thank you.

 

[jncarter]

This type of problem is much easier to do using Lagrangian mechanics. Are you familiar with this method? You could also set this up as an eigenvalue problem. You would use $\omega^{2}$ as your eigenvalue and $x_{1}, x_{2}$ as your eigenvector. You should find that there are two very distinct modes of motion given by the two possible values of $\omega$. In one case $x_{1}, x_{2}$ move in step with equal amplitudes. In the other case the two move out of phase with twice the amplitude of the first case. (If I remember my mechanics class correctly).

This problem is worked through in its entirety in Taylor. Further, this link appears to work through the problem in the case of equal masses, equal springs
http://www.physics.usu.edu/riffe/3750/Lecture 3.pdf

 

[99wattr89]

This type of problem is much easier to do using Lagrangian mechanics. Are you familiar with this method? You could also set this up as an eigenvalue problem. You would use $\omega^{2}$ as your eigenvalue and $x_{1}, x_{2}$ as your eigenvector. You should find that there are two very distinct modes of motion given by the two possible values of $\omega$. In one case $x_{1}, x_{2}$ move in step with equal amplitudes. In the other case the two move out of phase with twice the amplitude of the first case. (If I remember my mechanics class correctly).

This problem is worked through in its entirety in Taylor. Further, this link appears to work through the problem in the case of equal masses, equal springs
http://www.physics.usu.edu/riffe/3750/Lecture 3.pdf

I've had lectures on Lagrangian mechanics, but even after the lectures I still don't have a clue how it works, so that probably wouldn't be very fruitful. I also don't have a copy of Taylor sadly.

The derivation you linked uses the same sort of method as the one I followed to get to this point, but the matrix method is new. Thank you for linking it - following it I got to the answer for the first part of the question.

For the second part I got that the amplitudes were A = 0.5(1-√3)B and A = 0.5(1+√3)B for ω²₊ and ω²_- respectively. (A = x₁ amplitude, B = x₂ amplitude.

Unfortunately that creates a problem for part 3 - if A and B are related by a factor of 0.5(1±√3) then that seems to prevent a solution. Because it says that x₁ = x₀ and x₂ = 0.

So if x₂ = 0 at t=0, that means that since x₂ = Be^iωt, that B must equal zero. But that means that there's no oscillation at all, because A is a multiple of B!

 

[jncarter]

Include a phase factor in your solution.
$x_{1} = A*e^{i (\omega t +\delta_{1})}$
Similarly for the second wave vector. Now retain the amplitude relationships and use the phase factor $\delta$ to allow for zero values at time t=0. It may be more useful to use sine or cosine functions at this point because the exponential function is only zero as $\delta$ approaches negative infinity. The trigonometric functions, on the other hand, can equal zero.

 

[ehild]

I began with F=ma, and wrote down the equations of motion for each of the masses.

a) 2mx^..₁ = -kx₁ -k(x₁ -x₂)

and

b) mx^..₂ = -kx₂ +k(x₁ -x₂)


Then I added b to a, and subtracted b from a to get;

c) m(2x^..₁ +x^..₂) = -k(x₁ +x₂)

and

d) m(2x^..₁ -x^..₂) = -3k(x₁ -x₂)


Then I added d to c, and subtracted d from c to get;

e) mx^..₁ = -kx₁

and

f) mx^..₂ = kx₁ -2kx₂

You made a mistake in e). It should be the same as the original equation a).

The general motion of such a coupled vibrating system is the linear combination of the normal modes: collective SHM of the particles with the same frequency and defined ratio of amplitudes.

Suppose the displacements as $x_1=A_1e^{i\omega t}$, $x_2=A_2e^{i\omega t}$. You get a linear homogeneous system of equations for A₁ and A₂ which has non-zero solutions for certain ω values. Replace back these ω-s and you get the ratio of amplitudes for the normal mode with angular frequency ω. The general solution is linear combination of the normal modes belonging to the different angular frequencies and different relative amplitudes for x₁ and x₂.

ehild

 

[ehild]

For the second part I got that the amplitudes were A = 0.5(1-√3)B and A = 0.5(1+√3)B for ω²₊ and ω²_- respectively. (A = x₁ amplitude, B = x₂ amplitude.

Choose B=1. You can consider the normal modes as two-dimensional vectors: [A⁺,1]exp(iω⁺t) and [A^-,1]exp(-iω⁺t) and the general solution is a linear combination of them.

That is:
x₁=aA⁺exp(iω⁺t)+bA^-exp(iω^-t),

x₂=aexp(iω⁺t)+bexp(iω^-t).

ehild

 

[99wattr89]

Thank you for your replies!

Include a phase factor in your solution.
$x_{1} = A*e^{i (\omega t +\delta_{1})}$
Similarly for the second wave vector. Now retain the amplitude relationships and use the phase factor $\delta$ to allow for zero values at time t=0. It may be more useful to use sine or cosine functions at this point because the exponential function is only zero as $\delta$ approaches negative infinity. The trigonometric functions, on the other hand, can equal zero.

The goal is to find A and B, right?

How do you use the phase factor to solve the equations? I mean, what calculation do you do with it to make this work?

You made a mistake in e). It should be the same as the original equation a).

The general motion of such a coupled vibrating system is the linear combination of the normal modes: collective SHM of the particles with the same frequency and defined ratio of amplitudes.

Suppose the displacements as $x_1=A_1e^{i\omega t}$, $x_2=A_2e^{i\omega t}$. You get a linear homogeneous system of equations for A₁ and A₂ which has non-zero solutions for certain ω values. Replace back these ω-s and you get the ratio of amplitudes for the normal mode with angular frequency ω. The general solution is linear combination of the normal modes belonging to the different angular frequencies and different relative amplitudes for x₁ and x₂.

ehild

I don't quite get a when I retry e, I get 2mx^..₁ = -k(2x₁-x₂

But I've pretty much given up on that original method anyway, since I didn't get anywhere with it.

I'm sorry so say that I don't wholly understand what you're saying.

What is a linear homogeneous system of equations? Is that two coupled differential equations which are both linear and equal to zero? If so, how do I get them?

Choose B=1. You can consider the normal modes as two-dimensional vectors: [A⁺,1]exp(iω⁺t) and [A^-,1]exp(-iω⁺t) and the general solution is a linear combination of them.

That is:
x₁=aA⁺exp(iω⁺t)+bA^-exp(iω^-t),

x₂=aexp(iω⁺t)+bexp(iω^-t).

ehild

So, is what I have so far correct? Are a and b more constants? I thought A and B were the only constants you needed, why would there be two new ones? Also, if A and B aren't the only constants, then how do you set their values?

Assuming they are more constants, how do you use those expressions for x_{1, 2} to find the displacements as a function of time? Do you just need to find the four constants? If so, how does one do that?

 

[ehild]

You have found the frequencies the system can vibrate with, and the relation of the amplitudes of the separate masses. ω⁺ and ω^- are the angular frequencies of two special vibration of the system: when both masses vibrate with the same frequency and phase constant at a fixed ratio of their amplitudes. Such normal modes can be considered as the basis of a two-dimensional vector field of possible motions of the system of the masses and springs. The general motion is linear combination of these normal modes.

Using + and – to distinguish between the normal modes, the displacement of the masses are

$x_1^+=A^+\cos(\omega^+t+\phi^+)$
$x_2^+=B^+\cos(\omega^+t+\phi^+)$
$A^+=0.5(1-\sqrt{3})B^+$in case of the mode with ω⁺ angular frequency, and

$x_1^-=A^-\cos(\omega^-t+\phi^-)$
$x_2^-=B^-\cos(\omega^-t+\phi^-)$.
$A^-=0.5(1+\sqrt{3})B^-$

One of the amplitudes in both modes is arbitrary: You have chosen the B-s.

The general motion (I will denote the displacements by capital X1, X2) is linear combination of these modes. As the B-s are arbitrary they can be considered as the constants of the linear combination.

$X_1(t)=A^+\cos(\omega^+t+\phi^+)+A^-\cos(\omega^-t+\phi^-)$
$X_2(t)=B^+\cos(\omega^+t+\phi^+)+B^-\cos(\omega^-t+\phi^-)$You need to find B⁺,B^- and the phase constants from the initial conditions: X₁(0)=x₀, X₂(0)=0, dX₁(0)/dt=dX₂(0)/dt=0. ehild

 

[wotanub]

I don't know if you understand how to solve the problem yet, OP, but I just wanted to pop into say that the phase factor is unneeded. Since we're dealing with normal modes here, the two masses will either be completely in phase, or completely out of phase. In the case of being 180 degrees out of phase, they'll just be a negative sign in there.

Also, instead of guessing a solution with a sine and cosine for your DEs, just guess
$x_{1} = Acos(ωt)$
$x_{2} = Bcos(ωt)$

because that's just the real part of a complex exponential guess, and you don't need the imaginary part since you don't need to find velocities.

EDIT: I like this problem a lot, so I decided to work it the way you gave up on to show you what you could have did. I uploaded pics of my work to imgur since they're huge.

http://i.imgur.com/38KBL.jpg
http://i.imgur.com/xBzp9.jpg

I'll let you do the hard work on the third part of the problem using the initial conditions.

The reason I like this problem so much is I just learned how to do it yesterday! MIT OCW taught me how. http://ocw.mit.edu/courses/physics/8-03-physics-iii-vibrations-and-waves-fall-2004/video-lectures/lecture-5/ (not to advertise or anything...).

 

[ehild]

wotanub,

Your solution is nice, but I have noticed that you used the same notation (x1,x2) for the displacement in a normal mode and in the final solution. They are not the same!
The phase factor is not needed for the normal modes, but it has to be included at the final solution to fulfil the initial conditions.
As the solution gives the square of the angular frequency, the general solution contains both a sine and cosine term for both normal modes, or a cosine(sine) with phase factor.
The present initial conditions (zero initial velocities) result in zero phase constants. If there are nonzero initial velocities, pure cosine terms would not do. (Why?)

ehild

 

[wotanub]

Perhaps my notation it's a bit off my mistake. Thanks for taking notice.
I'm not sure what you're implying about the solution giving the square of the frequency. If you take the square root of the omega squared, you'd get plus or minus some number. Those are both frequencies, but since cos(-x) = cos(x), the four tems would simplify to two anyway. Was that your concern or is it that my solution is too specific? I don't think the problem gives enough information to solve for the phase angles if they were nonzero anyway. Do not quote me on that though, I've already put my notebook away.

 

[ehild]

I'm not sure what you're implying about the solution giving the square of the frequency. If you take the square root of the omega squared, you'd get plus or minus some number. Those are both frequencies, but since cos(-x) = cos(x), the four tems would simplify to two anyway. Was that your concern or is it that my solution is too specific? I don't think the problem gives enough information to solve for the phase angles if they were nonzero anyway. Do not quote me on that though, I've already put my notebook away.

Your solution is too specific. The general solution of the differential equation implies both exp(iωt) and exp(-iωt) (in complex notation) or both sin(ωt) and cos(ωt) or cosine/sine with a phase factor.

The solution in my post #8 can be fitted to any initial conditions.

ehild

 

[99wattr89]

You have found the frequencies the system can vibrate with, and the relation of the amplitudes of the separate masses. ω⁺ and ω^- are the angular frequencies of two special vibration of the system: when both masses vibrate with the same frequency and phase constant at a fixed ratio of their amplitudes. Such normal modes can be considered as the basis of a two-dimensional vector field of possible motions of the system of the masses and springs. The general motion is linear combination of these normal modes.

Using + and – to distinguish between the normal modes, the displacement of the masses are

$x_1^+=A^+\cos(\omega^+t+\phi^+)$
$x_2^+=B^+\cos(\omega^+t+\phi^+)$
$A^+=0.5(1-\sqrt{3})B^+$


in case of the mode with ω⁺ angular frequency, and

$x_1^-=A^-\cos(\omega^-t+\phi^-)$
$x_2^-=B^-\cos(\omega^-t+\phi^-)$.
$A^-=0.5(1+\sqrt{3})B^-$

One of the amplitudes in both modes is arbitrary: You have chosen the B-s.

The general motion (I will denote the displacements by capital X1, X2) is linear combination of these modes. As the B-s are arbitrary they can be considered as the constants of the linear combination.

$X_1(t)=A^+\cos(\omega^+t+\phi^+)+A^-\cos(\omega^-t+\phi^-)$
$X_2(t)=B^+\cos(\omega^+t+\phi^+)+B^-\cos(\omega^-t+\phi^-)$


You need to find B⁺,B^- and the phase constants from the initial conditions: X₁(0)=x₀, X₂(0)=0, dX₁(0)/dt=dX₂(0)/dt=0.


ehild

I think I see why. X_1,2 represent the changing position of the two masses over time as a combination of the normal modes, and the magnitude of each mode relative to the other is determined by the A and B values.

But how do you find the B values and phase constant? Everything I've read or looked up never explains the process for solving any of this, it just says 'and then you solve it'. I'm getting desperate, since this question and the other I posted about have eaten more than two weeks of my time now, and I have a lot more work I have to do before Friday (the deadline).

I don't know if you understand how to solve the problem yet, OP, but I just wanted to pop into say that the phase factor is unneeded. Since we're dealing with normal modes here, the two masses will either be completely in phase, or completely out of phase. In the case of being 180 degrees out of phase, they'll just be a negative sign in there.

Also, instead of guessing a solution with a sine and cosine for your DEs, just guess
$x_{1} = Acos(ωt)$
$x_{2} = Bcos(ωt)$

because that's just the real part of a complex exponential guess, and you don't need the imaginary part since you don't need to find velocities.

EDIT: I like this problem a lot, so I decided to work it the way you gave up on to show you what you could have did. I uploaded pics of my work to imgur since they're huge.

http://i.imgur.com/38KBL.jpg
http://i.imgur.com/xBzp9.jpg

I'll let you do the hard work on the third part of the problem using the initial conditions.

The reason I like this problem so much is I just learned how to do it yesterday! MIT OCW taught me how. http://ocw.mit.edu/courses/physics/8-03-physics-iii-vibrations-and-waves-fall-2004/video-lectures/lecture-5/ (not to advertise or anything...).

I followed through your working, but I think you made a mistake early on, and got a minus sign where there should be a plus in the initial equation 1, because your method is the same as mine but for that, and I get a different relationship between A and B.

Unfortunately I have absolutely no clue how to do the third part of the question.

 

[ehild]

Plug in t=0 into the expressions for X1(t) and X2(t). You get:

$X_1 (0)=A^+\cos(\phi^+)+A^-\cos(\phi^-)=x_0$
$X_2 (0)=B^+\cos(phi^+)+B^-\cos(\phi^-)=0$

$B^-\cos(phi^-)=-B^+\cos(\phi^+)$

Use the relation between the A-s and B-s, you get

$B^+\cos(phi^+)=-x_0/\sqrt{3}$
$B^-\cos(phi^+)=x_0/\sqrt{3}$

Do the same with the derivatives:
$\dot X_1 (0)=-A^+ \omega^+\sin(\phi^+)-A^-\omega^-\sin(\phi^-)=0$

$\dot X_1 (0)=-B^+ \omega^+\sin(\phi^+)-B^-\omega^-\sin(\phi^-)=0$

$B^- \omega^-\sin(\phi^-)=-B^+\omega^+\sin(\phi^+)$

$-0.5 B^+ (1-\sqrt{3})\omega^+\sin(\phi^+)+0.5 (1+\sqrt{3})B^+\omega^+\sin(\phi^+)=0 \rightarrow \phi^+=0, \phi^-=0$

ehild

 

[99wattr89]

Thank you very very much!

Plug in t=0 into the expressions for X1(t) and X2(t). You get:

$X_1 (0)=A^+\cos(\phi^+)+A^-\cos(\phi^-)=x_0$
$X_2 (0)=B^+\cos(phi^+)+B^-\cos(\phi^-)=0$

$B^-\cos(phi^-)=-B^+\cos(\phi^+)$

Use the relation between the A-s and B-s, you get

$B^+\cos(phi^+)=-x_0/\sqrt{3}$
$B^-\cos(phi^+)=x_0/\sqrt{3}$

Do the same with the derivatives:
$\dot X_1 (0)=-A^+ \omega^+\sin(\phi^+)-A^-\omega^-\sin(\phi^-)=0$

$\dot X_1 (0)=-B^+ \omega^+\sin(\phi^+)-B^-\omega^-\sin(\phi^-)=0$

$B^- \omega^-\sin(\phi^-)=-B^+\omega^+\sin(\phi^+)$

$-0.5 B^+ (1-\sqrt{3})\omega^+\sin(\phi^+)+0.5 (1+\sqrt{3})B^+\omega^+\sin(\phi^+)=0 \rightarrow \phi^+=0, \phi^-=0$

ehild

So the phi terms have to be zero because the coefficients are non-zero and sum to root3 times B⁺ω⁺, meaning that the sin terms have to both be zero for all values of B and ω. Is that right?

And should the final answer be left in terms of B and not x₀ or something like that?

 

[ehild]

So the phi terms have to be zero because the coefficients are non-zero and sum to root3 times B⁺ω⁺, meaning that the sin terms have to both be zero for all values of B and ω. Is that right?

Yes.

And should the final answer be left in terms of B and not x₀ or something like that?

The final answer should include xo.


ehild

 

[99wattr89]

Yes.


The final answer should include xo.


ehild

Thank you again for all your help!