- #1
Ray Fischer
- 17
- 0
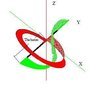
I have made a geometry, see first attachment, I call the “Torbus”, from the two geometries of a Toroid and a Mobius ring, though the twisted ring cut from a torus is not the classical Mobius ring. I have not been able to derive the math (too many variables) that describes the movement of the twisted ring relative to the torus; though I have been able, from a model, to determine the movement of two unique points separated 1800 on the twisted ring. One point (red) travels 7200 through the torus and the other (green) travels around the torus 3600. I need help deriving the math. The animation on my website (myspace/torbuspuzzles) shows the twisted ring’s movement relative to the torus. In attachment 2 is a drawing of what the loci of the two points appear to be. The two points , red and green, are at opposite ends of what I call a “Torbus Baton” see attachment 3.
A thought:
A thought:
Attachments
Last edited by a moderator: