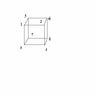
- #1
EG
- 5
- 0
has anyone investigated the three-d scattering of numbers?
FYI:
for any base
take the symbols that represent the numbers
arrange them in a rectangular or square grid
from a starting point, follow them in a square, rectangle, or diamond until you construct a number of 2n digits
divide by a number consisting of n "1" ' s
and there is no remainder.
Probably falls out of some other findings, but an interesting construction.
EG
FYI:
for any base
take the symbols that represent the numbers
arrange them in a rectangular or square grid
from a starting point, follow them in a square, rectangle, or diamond until you construct a number of 2n digits
divide by a number consisting of n "1" ' s
and there is no remainder.
Probably falls out of some other findings, but an interesting construction.
EG