Exploring the Wedge Product & its Role in Vectors & Orthogonality

[sponsoredwalk]

I think I finally understand the wedge product & think it explains things
in 2-forms that have been puzzling me for a long time.

My post consists of the way I see things regarding the wedge product & interspersed with
my thoughts are only 3 questions (in bold!) that I'm hoping for some clarification on.
The rest of the writing is just meant to be read & hopefully it's all right, if it's wrong do
please correct me

If
v = v₁e₁ + v₂e₂
w = w₁e₁ + w₂e₂

where e₁ = (1,0) & e₂ = (0,1) then

v ⋀ w = (v₁e₁ + v₂e₂) ⋀ (w₁e₁ + w₂e₂)
_____ = v₁w₁e₁⋀e₁ + v₁w₂e₁⋀e₂ + v₂w₁e₂⋀e₁ + v₂w₂e₂⋀e₂
_____ = v₁w₂e₁⋀e₂ + v₂w₁e₂⋀e₁
v ⋀ w= (v₁w₂ - v₂w₁)e₁⋀e₂

This is interpreted as the area contained in v & w.

My first question is based on the fact that this is a two dimensional calculation
that comes out with the exact same result as the cross product of
v'_= v₁e₁ +_v₂e₂_+ 0e₃
w' = w₁e₁ + w₂e₂ + 0e₃

Also the general x ⋀ y = (x₁e₁ + x₂e₂ + xe₃) ⋀ (y₁e₁ + y₂e₂ + ye₃)
comes out with the exact same result as the cross product.

In all cases the end result is a vector orthogonal to v & w, or to v'& w',
or to x'& y'. Is this true for every wedge product calculation in every
dimension? The wedge product of two vectors in ℝ³ gives the area
of parallelogram they enclose & it can be interpreted as a scaled up factor
of a basis vector orthogonal to the vectors. So (e₁⋀e₂) is an orthogonal
unit vector to v & w & (v₁w₂ - v₂w₁) is a scalar that also gives the area
enclosed in v & w.

Judging by this you'd take the wedge product of 3 vectors in ℝ⁴ &
get the volume they enclose, and 4 vectors in ℝ⁵ gives hypervolume or
whatever. If we ended up with β(e₁⋀e₂⋀e₃) this would be in ℝ⁴ where β is
the scalar representing the volume & β(e₁⋀e₂⋀e₃) is pointing off into
the foursth dimension whatever that looks like. If all of this holds I can
justify why e₁⋀e₂ = - e₂⋀e₁ both mentally & algebraically by taking dot
products & finding those orthogonal vectors so I'd like to hear if this
makes sense in the grand scheme of things!

I really despise taking things like e₁⋀e₂ = - e₂⋀e₁ as definitions unless I
can justify them. I can algebraically justify why e₁⋀e₂ = - e₂⋀e₁ by
thinking in terms of the cross product which itself is nothing more than
clever use of the inner product of two orthogonal vectors. Therefore I
think that e₁⋀e₂ literally represents the unit vector that is orthogonal to
the vectors v & w involved in my calculation. So if there are n - 1 vectors
then e₁⋀e₂⋀...⋀en lies in ℝⁿ and is the unit vector as part of some
new vector βe₁⋀e₂⋀...⋀en that is orthogonal to (n - 1) vectors.

I read a comment that the wedge product is in an "exterior square" so I
guess this generalizes to products of all arity (exterior volumes et al) &
from browsing I've seen that a "bivector" is a way to interpret this, like
this:

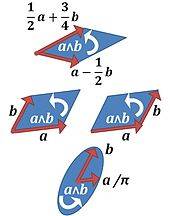
it's a 2 dimensional vector here for example. My second question is -
if I were to just think in terms of orthogonality as I have explained
in this thread is there any deficiency? As far as I can tell this 2-D
vector in the picture is just a visual representation of the area & as it is
explained via a scaled up orthogonal vector I think there is virtually no difference.

A lot of the wiki topics on "bivectors" and forms etc... were previously
unreadible to me & are only now slowly beginning to make sense (I hope!).

And finally, I'm hoping to use this knowledge above (assuming it's right) to try to
understand terms like

Adx + Bdy + Cdz
&
Adydz + Bdzdx + Cdxdy

in this context. I've seen calulation that specifically require dxdx = dydy = dzdz = 0 &
you're supposed to remember this magic but I don't buy it as just magic, I think there are
very good reasons why this is the case. My third question arises from the fact that I think
these algebraic rules, like dxdy = -dydx & dxdx = 0 etc... are just encoding within
them rules that logically follow from everything I've explained above & would probably be
more clearly delineated through vectors, are they encoding vector calculations dealing
with orthogonality?
Perhaps someone more knowledgeable could expand upon this, I'd greatly appreciate it.

 

[Hurkyl]

I really despise taking things like e₁⋀e₂ = - e₂⋀e₁ as definitions unless I
can justify them.

You're reading too much into the label "definition". Just because the author called this a definition doesn't mean it's more special than any other property wedge products might have.

The author labeled it a definition for the sake of pedagogy and/or for convenience -- he thought it was easier to present the subject taking this as a starting point.



The secret thing going on here is as follows: for an n-dimensional vector space, the vector space of n-vectors (i.e. wedge products of n vectors) is one-dimensional. If you choose an (ordered) basis {e_i} for V, then the n-vector e₁⋀...⋀e_n is nonzero, and so forms a basis for the space of n-forms.

So now, you can play a game where you pretend n-vectors are just scalars. For clarity, if w is an n-formvector then I'll write *w to denote the corresponding scalar. (i.e. the coordinate of W with respect to the chosen basis)

With some thought, you can see the space of (n-1)-vectors is n-dimensional, so if we choose a basis we can pretend they are actually vectors of V. If f is an (n-1)-vector, I will use *f to denote the vector we are pretending it to be.

The usual way to set things up, I think, works out so that *(f ⋀ u) is the dot product of *f with u.

In ℝ³, it works out that *(u⋀v). So I think with this you can confirm the observations you were making.

Incidentally, * is called the Hodge dual.



In 3 dimensions, these tricks can turn everything into scalars and vectors, which probably explains why vector calculus was invented before wedge products and n-vectors and n-forms were invented. However, in four or more dimensions you can't get rid of 2-vectors in this fashion. Nor can you get rid of 3-vectors in five or more dimensions, and so forth.

In 4 or more dimensions, things are even worse -- most 2-vectors cannot be written as u⋀v for a pair of vectors u and v. The best you can do in four dimensions, I think, is to write them as

u⋀v + x⋀y​

for four vectors u,v,x,y.
(I'm not sure if you can get away with just two terms in the above sum -- you might need more, even in four dimensions)



But it is useful sometimes to think about n-vectors as n-vectors, even in 3-dimensional space when you can play the above tricks to convert everything into a scalar or a vector.

The definition of n-vector doesn't involve an inner production any fashion, and so it is useful in situations where you don't have an inner-product, or you are considering several inner-products, or the inner-product is inconvenient to use.

The definition of n-vector also captures some geometrical information -- e.g. if we use standard coordinates on the Euclidean plane and reflect it across the line x=y, this should do nothing to scalars and swap the coordinates of any vector. A quick calculation shows that this also multiplies any 2-vector by -1.

The important thing to notice now is that the reflection of the wedge product of u and v is the same as the wedge products of the reflections of u and v. However, the reflection of the cross product of u and v is not the cross product of the reflections of u and v.

If you've ever heard the terms pseudovector and pseudoscalar, they are referring to this phenomenon. Effectively, when someone write down a vector and says it's a pseudovector, they are saying "I don't really mean the vector I just wrote -- instead I am am talking about the 2-vector whose Hodge dual is the vector I just wrote".



Incidentally, there's a similar game that converts between "form" and "vector".

 

[sponsoredwalk]

Hurkyl you're going too fast for me :tongue2:

I take it that what I wrote didn't offend your senses so at least most of it isn't wrong.

I asked three specific questions because I feel I will be able to understand more about
this subject by using the questions I've asked here as my foundation.
My eyes can't help but glaze over when reading all of the threads on PF, all of the wiki
pages & all of the many books on googlebooks on forms.

You're reading too much into the label "definition". Just because the author called this a definition doesn't mean it's more special than any other property wedge products might have.

The author labeled it a definition for the sake of pedagogy and/or for convenience -- he thought it was easier to present the subject taking this as a starting point.

This is a separate issue but a very important one, an example will make this clear.
If I define a function φ that satisfies

1) φ(0) = 0 &
2) (φ(x) = 0) ⇒ (x = 0)
3) φ(x + y) ≤ φ(x) + φ(y)
4) φ(ax) = |a|φ(x)

and call it a norm that's great. But especially axiom 3), the triangle inequality, I mean that
is derivable from scratch & provable. Furthermore I most certainly could not make sense
of what this was saying or why anybody cared about it until I was able to derive & prove
it. It's the exact same with forms now, I just can't accept things like e₁⋀e₂ = - e₂⋀e₁
until I can derive them. I think I have but I want to be sure. But I just can't understand
anything beyond this at this moment.

 

[Hurkyl]

Generally, it doesn't make direct sense to ask if (v ⋀ w) is orthogonal to v, they are very different sorts of things.

Orthogonality enters into play in a form of duality -- in three dimensions, for example, there are two ways to describe a plane through the origin. On the one hand, you could specify two (non-parallel) lines lying in the plane. On the other hand, you could specify a line perpendicular to the plane.

Like a 1-vector specifies a line, orientation, and magnitude, a (pure) 2-vector is essentially specifying a plane, orientation, and magnitude. Using the wedge product of two 1-vectors to produce a 2-vector is analogous to specifying two lines to define a plane.

The orthogonality you mention comes from the other description -- the analog to specifying the plane by the line perpendicular to it.


In seven dimensions, lines and 6-dimensional shapes are dual. So by duality you could view a 6-vector as if it was a vector... but you could not view a 2-vector as if it were a vector. However, in seven dimensions, there is a duality between 2-vectors and 5-vectors.

 

[homology]

I really despise taking things like e₁⋀e₂ = - e₂⋀e₁ as definitions unless I
can justify them

I understand. I often suffer the same need. But sometimes its worth putting aside such things until you're ready. The antisymmetry of the wedge product comes about through its construction. The wedge of two vector spaces is a quotient space of their tensor product. You mod out by the relation $$v\tensor v$$.

I know there's a good reason why we want antisymmetric tensors...but I can't recall it (Hurkyl most certainly would know as would a number of others on this forum). Though one good reason might be that while the tensor algebra for a manifold contains an infinite number of spaces the wedge algebra doesn't...

In any event, such things as the construction of the wedge algebra won't help you compute or figure out how its related to traditional vector analysis. Just jot it down as a question to be determined later and plow on for now. :)

 

[Landau]

If I define a function φ that satisfies

1) φ(0) = 0 &
2) (φ(x) = 0) ⇒ (x = 0)
3) φ(x + y) ≤ φ(x) + φ(y)
4) φ(ax) = |a|φ(x)

and call it a norm that's great. But especially axiom 3), the triangle inequality, I mean that
is derivable from scratch & provable.

From scratch? Really?
If I define $\phi:\mathbb{R}^2\to \mathbb{R}$ by $\phi(x,y)=-\sqrt{x^2+y^2}$ then it satisfies 1,2 and 4, but not 3.

It's the exact same with forms now, I just can't accept things like e₁⋀e₂ = - e₂⋀e₁
until I can derive them.

How are you going to derive something from nothing?

I suspect you are asking for more intuitive axioms from which you can derive less intuitive properties.

 

[sponsoredwalk]

Orthogonality enters into play in a form of duality -- in three dimensions, for example, there are two ways to describe a plane through the origin. On the one hand, you could specify two (non-parallel) lines lying in the plane. On the other hand, you could specify a line perpendicular to the plane.

Like a 1-vector specifies a line, orientation, and magnitude, a (pure) 2-vector is essentially specifying a plane, orientation, and magnitude. Using the wedge product of two 1-vectors to produce a 2-vector is analogous to specifying two lines to define a plane.

The orthogonality you mention comes from the other description -- the analog to specifying the plane by the line perpendicular to it.

This makes a good deal of sense. I really like the description of the plane as
N•(X - X₀) = 0
as it can be reduced to the standard equations & encodes a lot of material that can
easily be reconstructed. This is exactly what I'm talking about when I mentioned the

Adx + Bdy + Cdz
&
Adydz + Bdzdx + Cdxdy

stuff at the end of my OP. specifically, if you check Edwards "Advanced Calculus A
Differential Forms Approach" he is explicitly using this material in it's scalar form.
He explicitly defines dxdx = dydy = dzdz = 0.

What I am trying to find is a general way to look at forms in a way that both the
anti-symmetric character & the "dzdz = 0 character" explicitly fall out of calculations
(such as is done in the cross product .pdf's in the links I gave) thus offering an
actual explanation within the context of orthogonality..

That's all, I think there's something like this I just haven't realized yet. I've rewritten
my post in a far clearer manner than before so I hope that's clearer.

I know there's a good reason why we want antisymmetric tensors...

I don't doubt it, but why accept something as definition that seems strange when it can
be derived? As an example I mention ∑₁ⁿk = n(n + 1)/2. Why bother going any further with
this than accepting the mathematical induction proof of this? I mean, the proof validates
it so why care? Personally this formula was unacceptable to me until I read Gauss' derivation:
S = 1 + __2 __ + ... + n
S = n + (n - 1) + ... + 1
2S = n(n + 1)
S = n(n + 1)/2.

Similarly the anti-symmetric property of the cross product can be derived through some
laborious (but satisfying) algebra. This holds for ∑₁ⁿk² etc...

There are always multiple explanations for these things, I have a thread on matrix
multiplication with four or five alternative justifications.

 

[sponsoredwalk]

From scratch? Really?

If you want to start from basic logic, construct a system of logic, construct set axioms
consistent with your rules of logic, go on to define/derive/prove all of the mathematical
constructs preceeding the optimal point at which the Triangle Inequality needs to be
introduced then yes it is derivable "from scratch" (which I think you are well aware meant
within a mathematical framework).

If I define $\phi:\mathbb{R}^2\to \mathbb{R}$ by $\phi(x,y)=-\sqrt{x^2+y^2}$ then it satisfies 1,2 and 4, but not 3.How are you going to derive something from nothing?

I suspect you are asking for more intuitive axioms from which you can derive less intuitive properties.

I'm not looking for axioms I'm trying to understand the aspects of the wedge product and
differential forms that I mentioned in my OP that appear to arise naturally in vector analysis
(producing the same results in ℝ² & ℝ³) from looking at the concept of orthogonality.
I've rewritten that post to be far clearer so hopefully you'll see what I mean, I apologise
for not getting it right the first time.

I mentioned the triangle inequality for a reason. You can take it as an axiom in the
context of my φ function but in the context of the real number system (for example)
it can be proven based on the axioms for the real number system. The whole point I was
making was that the inequality can be derived in a more fundamental context upon which
axiomatizing it (in the φ context) is justified. Similarly to define i x j = k
and i x i = 0 & j x i = -k in the context of the cross
product is just too much for me when I can algebraically show that this holds by
using the concept of orthogonality (the cross product sections in the following two links:
1 & 2, make this explicit).

Anyway, very little of this has anything to do with forms or the wedge product.

 

[sponsoredwalk]

The responses in this thread don't really attack what I was asking about, that was
my fault for not making my original post clearer. I've rewritten it as follows: first a
look at the cross product; then a look at a wedge product calculation & it's similarities
(that I think are far more explicit if you interpret it in the way I've explained below) to
the cross product & finally 5 questions (in bold) that are motivated by the wedge product
calculation with unbolded text just elaborating on the question just in case.

----

The cross product is a strange animal, it really has very little justification as it is
taught in elementary linear algebra books. It took me a long time to learn that the
cross product is really no more than the dot product in disguise. It is actually quite
easy to derive the result that a cross product gives, through clever algebra, as is done
in the cross product pdf's here & here.
By doing your own algebra you can justify the anti-symmetric property of the cross product,
$$\overline{u} \ x \ \overline{v} \ = \ - \ \overline{v} \ x \ \overline{u}$$

So understanding the cross product in this way is quite satisfying to me as we can
easily justify why $$\overline{u} \ x \ \overline{u} \ = \ 0$$ without relying
on these properties as definitions.

My questions are based on the fact that these properties can be justified in such an
elementary way. If you've never seen the cross product explained they way it is in
the .pdf's then I urge you to read them & think seriously about it. I'm sure these are
justified in more advanced works in other ways but if an explanation can be given
at this level I see no reason not to take it.

So let's look at an example & the steps taken that I think have explanations analogous
to those of the cross product above:

v = v₁e₁ + v₂e₂

w = w₁e₁ + w₂e₂

where e₁ = (1,0) & e₂ = (0,1).

v ⋀ w = (v₁e₁ + v₂e₂) ⋀ (w₁e₁ + w₂e₂)
_____ = v₁w₁e₁⋀e₁ + v₁w₂e₁⋀e₂ + v₂w₁e₂⋀e₁ + v₂w₂e₂⋀e₂
_____ = v₁w₂e₁⋀e₂ + v₂w₁e₂⋀e₁
v ⋀ w= (v₁w₂ - v₂w₁)e₁⋀e₂

This is interpreted as the area contained in v & w.
No doubt you noticed that all of the manipulations with the e terms have
the exact same form as the cross product. Notice also the fact that this two
dimensional calculation comes out with the exact same result as the cross product of

v'_= v₁e₁ +_v₂e₂_+ 0e₃
w' = w₁e₁ + w₂e₂ + 0e₃
in ℝ³. Also the general

x ⋀ y = (x₁e₁ + x₂e₂ + xe₃) ⋀ (y₁e₁ + y₂e₂ + ye₃)

comes out with the exact same result as the cross product. The important thing is that
the cross product of the two vector results in a vector orthogonal to v & w and that the
result is the same as the wedge product calculation.

1: Can e₁ ⋀ e₂ be interpreted as e₃ in my above calculation?

What I mean is that can e₁ ⋀ e₂ be interpreted as a (unit) vector
orthogonal to the two vectors involved in the calculation that is scaled up by some
factor β, i.e. βe₁ ⋀ e₂ where β is the scalar representing the
area of the parallelogram.

2: Just as we can algebraically validate why $$\overline{u} \ x \ \overline{v} \ = \ - \ \overline{v} \ x \ \overline{u}$$
why doesn't the exact same logic validate
e₁ ⋀ e₂ = - e₁ ⋀ e₁?

If we think along these lines I think we can justify why e₁ ⋀ e₁ = 0,
just as it occurs analogously in the cross product. They seems far too similar for it
to be coincidence but I can't find anyone explaining this relationship.

3: In general, if you are taking the wedge product of (n - 1) vectors in n-space
will you always end up with a new vector orthogonal to all of the others?

If you are taking the wedge product of (n - 1) vectors then will you end up with
λ(e₁⋀e₂⋀...⋀en)
where the term (e₁⋀e₂⋀...⋀en) is orthogonal to all
the vectors involved in the calculation & the term λ represents the area/volume
/hypervolume (etc...) contained in the (n - 1) vectors?

4: I have seen it explained that we can interpret the wedge product of e₁ ⋀ e₂
as in the picture here, as a kind of two-dimensional vector.
Still, the result given is no different to that of the 3-D cross product so is it not
justifiable to think of e₁ ⋀ e₂ as if it were just an orthogonal vector in the
same way you would the cross product if you think along the lines I have been tracing
out in this post? When you go on to take the wedge product of (n - 1) vectors in n-space
can I not think in the same (higher dimensional) way?

5: Are calulations like dxdx = dydy = dzdz = 0, dxdy = -dydx etc...
just encoding within them rules that logically follow from calculations
dealing with orthogonality?

Since:
1) Adx + Bdy + Cdz & Adydz + Bdzdx + Cdxdy are differential forms,
2) a 1-form can be thought of analogous to the concept of work in physics,
3) work in physics can be formulated as a vector dot product,
4) the vector (cross) product actually encodes rules like i x i = j x j = k x k= 0, i x j = -j x i
which are so similar to dzdz = 0, dxdy = -dydx etc...

it seems far too much of a coincidence to me that things like e₁ ⋀ e₂ = - e₁ ⋀ e₁
need to be definitions when in the analagous vector formulations there are rich explanations
that are simply derived from orthogonality calculations (as in the pdf's). There must be a
general mode of approach to these questions in the wedge product/forms methods also
using concepts of orthogonality & there must be some way to show things like
e₁ ⋀ e₂ = - e₂ ⋀ e₁ and higher dimensional generalizations
just using orthogonality considerations.

That's it, thanks a lot for taking the time to read this I have tried to be as clear
as possible, any contradictions/errors are as a result of my poor knowledge of all of
this! :D

 

[homology]

It took me a long time to learn that the
cross product is really no more than the dot product in disguise.

Not sure what you mean here? typo? The cross product is certainly not a dot product.

So let's look at an example & the steps taken that I think have explanations analogous
to those of the cross product above:

v = v₁e₁ + v₂e₂

w = w₁e₁ + w₂e₂

where e₁ = (1,0) & e₂ = (0,1).

v ⋀ w = (v₁e₁ + v₂e₂) ⋀ (w₁e₁ + w₂e₂)
_____ = v₁w₁e₁⋀e₁ + v₁w₂e₁⋀e₂ + v₂w₁e₂⋀e₁ + v₂w₂e₂⋀e₂
_____ = v₁w₂e₁⋀e₂ + v₂w₁e₂⋀e₁
v ⋀ w= (v₁w₂ - v₂w₁)e₁⋀e₂

This is interpreted as the area contained in v & w.

So if we're worried about definitions, how are you defining the wedge product?

No doubt you noticed that all of the manipulations with the e terms have
the exact same form as the cross product. Notice also the fact that this two
dimensional calculation comes out with the exact same result as the cross product of

v'_= v₁e₁ +_v₂e₂_+ 0e₃
w' = w₁e₁ + w₂e₂ + 0e₃
in ℝ³. Also the general

x ⋀ y = (x₁e₁ + x₂e₂ + xe₃) ⋀ (y₁e₁ + y₂e₂ + ye₃)

comes out with the exact same result as the cross product. The important thing is that
the cross product of the two vector results in a vector orthogonal to v & w and that the
result is the same as the wedge product calculation.

You mean to say that the coefficients of what you did with wedges are the same as the coefficients of what you would do with a cross product.

1: Can e₁ ⋀ e₂ be interpreted as e₃ in my above calculation?

What I mean is that can e₁ ⋀ e₂ be interpreted as a (unit) vector
orthogonal to the two vectors involved in the calculation that is scaled up by some
factor β, i.e. βe₁ ⋀ e₂ where β is the scalar representing the
area of the parallelogram.

Hurkyl answered this with the statement about the Hodge Dual. Its a lucky coincidence for us that yes, there is an interesting correspondence between bivectors and vectors, but only in three dimensions. Also, realize that these objects are not the same geometrically. The wedge product will not change under reflection while the cross product will, the cross product depends on orientation while the wedge product doesn't. Things further become messy when we move to curvilinear coordinates and take the cross product to the level of the curl and so on.

2: Just as we can algebraically validate why $$\overline{u} \ x \ \overline{v} \ = \ - \ \overline{v} \ x \ \overline{u}$$
why doesn't the exact same logic validate
e₁ ⋀ e₂ = - e₁ ⋀ e₁?

If we think along these lines I think we can justify why e₁ ⋀ e₁ = 0,
just as it occurs analogously in the cross product. They seems far too similar for it
to be coincidence but I can't find anyone explaining this relationship.

So it seems that you're not looking for proof, just just a good explanation? Because seeing that two things look the same in one space for one set of coordinates and one orientation does not a proof make. Moreover, really you want to start with wedges and then prove stuff about cross products. Wedge products are more fundamental. Or if you're given to historical accuracy, start with the quaternions, that's where the cross product originally arose and Hamilton defined those using just a couple relations and all the rest of the cross product definitions fall out of that (i,j, and k are the unit quaternions, where each is a complex unit, so $$i^2=j^2=k^2=-1$$ and $$ijk=-1$$).

And since we're not proving anything and we're just creating good intuitive arguments: if you accept that the wedge product of two 1-forms can give you an area 'between' them then if you're using identical forms the area will be zero. Work out a calculation using a basis. But the point is, that the antisymmetry of the wedge product comes from its tensor construction not from vector analysis, though that may be a helpful way to think about it.

3: In general, if you are taking the wedge product of (n - 1) vectors in n-space
will you always end up with a new vector orthogonal to all of the others?

No, not in general. You could zero for example. If you're in a five dimensional space the wedge of a 3 form with a 4 form is zero. As another example, if you take a 1-form and a 2-form that'll give you a 3-form but its hodge dual will give you a 2-form so you'll have to think about what that means in terms of 'perpendicular'. Another detail worth mentioning here is that neither the wedge product nor the cross product result in the same kind of object you began with. For example, if you take two (contravariant) vectors and take their cross product, you don't get another (contravariant) vector. The new object behaves differently under transformations. So if you started in a space V, you're not still in that space after you take a cross product. Ditto for the wedge product. With the wedge product you have n spaces if your manifold is n-dimensional and they're 'graded' by the wedge product so there's a 1-wedge space, then a 2-wedge space, then a 3-wedge space, and so on all up the line until you get to the n-wedge space. You can take any two forms, maybe a p-form and a q-form (from different spaces because they're different critters) and take their wedge and as long as p+q is no greater than n you get another form belonging to the p+q-wedge space.

If you are taking the wedge product of (n - 1) vectors then will you end up with
λ(e₁⋀e₂⋀...⋀en)
where the term (e₁⋀e₂⋀...⋀en) is orthogonal to all
the vectors involved in the calculation & the term λ represents the area/volume
/hypervolume (etc...) contained in the (n - 1) vectors?

I've only ever seen it done with differential forms, but sure you'd have some stuff in $$\lambda$$depending on orientation and the metric, but sure.

4: I have seen it explained that we can interpret the wedge product of e₁ ⋀ e₂
as in the picture here, as a kind of two-dimensional vector.
Still, the result given is no different to that of the 3-D cross product so is it not
justifiable to think of e₁ ⋀ e₂ as if it were just an orthogonal vector in the
same way you would the cross product if you think along the lines I have been tracing
out in this post? When you go on to take the wedge product of (n - 1) vectors in n-space
can I not think in the same (higher dimensional) way?

It is different. The oriented area is not the same as a vector perpendicular to it. You can create a correspondence, but its not the identity. It doesn't general transformations. In higher dimensions you will need to talk about what is 'orthogonal' and in what way two forms are orthogonal.

5: Are calulations like dxdx = dydy = dzdz = 0, dxdy = -dydx etc...
just encoding within them rules that logically follow from calculations
dealing with orthogonality?

Not sure what you mean here? With your area interpretation $$dx\wedge dx=0$$ makes sense since for any vectors you give it, it'll just pluck out the 'x' components and give you the area spanned by two vectors with those components, which would be zero. The deeper reason is that you can have antisymmetry if $$dx\wedge dx\neq 0$$

it seems far too much of a coincidence to me that

Yes indeed, it is too much of a coincidence. This should cause you to look deeper into wedge products and find out where they come from because the justifications for their properties are more general than orthogonality (the presence of or even the concept). All of the properties of wedge products can be derived from very basic principles without even mentioning dot products, cross products, orthogonality, etc.

I hope the above helps :)

 

[sponsoredwalk]

Not sure what you mean here? typo? The cross product is certainly not a dot product.

I'll give the rest of your post serious thought & get back to you on it but please read the
pdf's in the links I gave that explain what I am talking about when I say the cross product
is nothing more than the dot product (and some clever algebra) in disguise.