- #1
stunner5000pt
- 1,461
- 2
A particle in a potnetial V(x) has a definite energy
[tex] E = - \frac{\hbar^2 \alpha^2}{2m} [/tex]
and its eigenfunction is given by
[tex] \psi(x) = Nx \exp(-alpha x) [/tex] if 0 <= x < infinity
zero elsewhere
Prove that [tex] V(x) = -alpha \hbar^2/mx [/tex] 0 <= x < infinity
infinity elsewhere
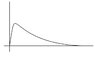
Given that the eigenfunction describes the ground state of the aprticle in teh potnetial V(x) roughly sketch the the eigenfunction whifchcdescribes the first excited state
ground state ook like sketch 1
no zeroes
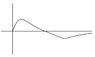
i think the first excited state will look like sketch
it has to have 1 zero...
[tex] E = - \frac{\hbar^2 \alpha^2}{2m} [/tex]
and its eigenfunction is given by
[tex] \psi(x) = Nx \exp(-alpha x) [/tex] if 0 <= x < infinity
zero elsewhere
Prove that [tex] V(x) = -alpha \hbar^2/mx [/tex] 0 <= x < infinity
infinity elsewhere
Given that the eigenfunction describes the ground state of the aprticle in teh potnetial V(x) roughly sketch the the eigenfunction whifchcdescribes the first excited state
ground state ook like sketch 1
no zeroes
i think the first excited state will look like sketch
it has to have 1 zero...