- #1
yre
- 18
- 0
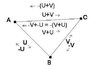
In special relativity, the velocity-addition for colinear velocities u and v is given by (u+v)/(1+uv/c^2), but for non-colinear velocities the formula is more complicated and is not symmetric in u and v. But since the reciprocal velocity of v is -v then the reciprocal of (u+v) should be -(u+v) but also starting from the other end the reciprocal should also be (-v + -u) however -(u+v) is not equal to (-v + -u) according to the addition formula. So what is going on?
The resolution of the velocity composition paradox as described at http://en.wikipedia.org/wiki/Velocity-addition_formula makes it clear that Einstein's original non-commutative velocity addition, that Einstein said only obeys the parallelogram law to first approximation, is not actually a velocity composition law - it is a boost parameter composition law which only partially describes boost composition.
Ungar has been writing about this since 1988, but given that it is well known that a boost followed by a boost results in a boost plus a rotation then I'm guessing that people familiar with boost composition must have known the fact that the original addition formula doesn't give the actual composite velocity, except when the velocities are colinear. So can anyone point to a reference prior to Ungar's work that explicitly states this fact ?
Attachments
Last edited: