- #1
qinglong.1397
- 108
- 1
Hello, everyone!
I'm studying Nakahara's book, Geometry, Topology and Physics and now studying the connection theory. I come across a problem. Please look at the two attachments.
In the attachment
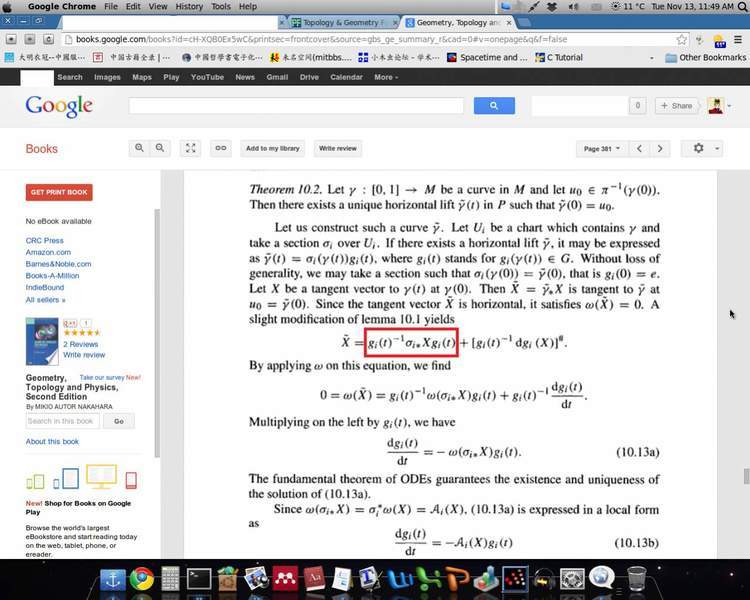 , Nakahara said we could use the similar method in the attachment
, Nakahara said we could use the similar method in the attachment
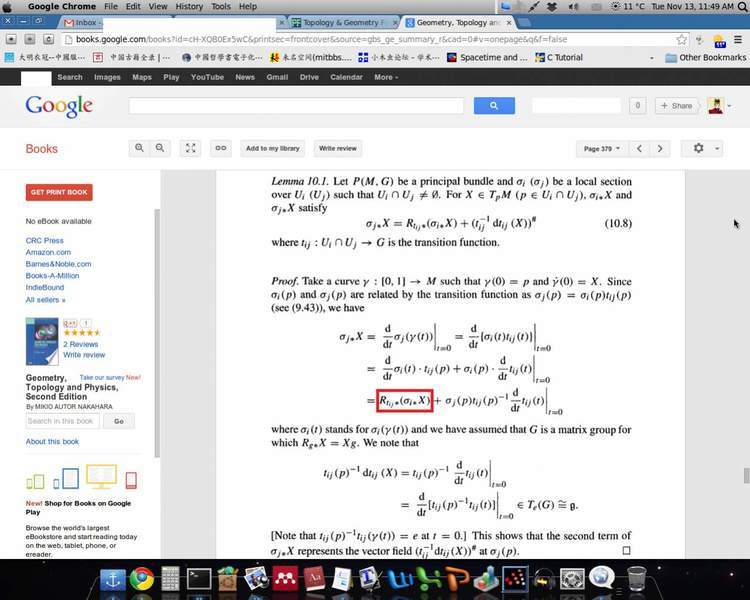 to get [itex]\tilde X[/itex], but why does the first term have [itex]g_i(t)^{-1}[/itex]. According to the first figure, the first term should have the following form
to get [itex]\tilde X[/itex], but why does the first term have [itex]g_i(t)^{-1}[/itex]. According to the first figure, the first term should have the following form
[itex]R_{g_i(t)*}\sigma_{i*}X[/itex]
Since [itex]R_{g*}X=Xg[/itex], it becomes
[itex](\sigma_{i*}X)g_i(t)[/itex]
So there shouldn't be [itex]g_i(t)^{-1}[/itex]. But why did the author put it there? Thank you!
I'm studying Nakahara's book, Geometry, Topology and Physics and now studying the connection theory. I come across a problem. Please look at the two attachments.
In the attachment
[itex]R_{g_i(t)*}\sigma_{i*}X[/itex]
Since [itex]R_{g*}X=Xg[/itex], it becomes
[itex](\sigma_{i*}X)g_i(t)[/itex]
So there shouldn't be [itex]g_i(t)^{-1}[/itex]. But why did the author put it there? Thank you!