A rod constrained at it's ends

[jncarter]

Homework Statement

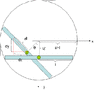
A thin rod of length 2l and linear mass density of $\lambda$ is constrained to move with its ends on a circle of radius a, where a>l. The circle is in the vertical plane (gravity is present). The contacts between the circle and rod are frictionless.

Part A: Write down the Lagrangian describing the motion of the rod.
Part B: Calculate the frequency of oscillation for small departures from equilibrium.

Homework Equations

The Lagrangian: L = $\frac{1}{2}mv^2$ + mgh. Where h is the height and is some function of the angle $\theta.$
The Euler-Lagrange equation: $\frac{d}{dt}$$\frac{\partial L}{\partial q}$ = $\frac{\partial L}{\partial \dot{q}}$

The Attempt at a Solution

The distance between the center of mass and the center of the circle (call it L) must remained fixed, the center of mass moves like a simple pendulum. Its Lagrangian is given by

$L = \lambda l L^2\dot{\theta}^2 - 2\lambda gLcos\theta$​

and would have a period of $\sqrt{\frac{L}{g}}$.
I can't tell if I have to describe the motion at some point $dl = \sqrt{dx^2 + dy^2}$from the center of mass (with coordinates $X=Lsin \theta$ $Y =Lcos \theta$. I think it comes down to a problem with understanding the geometry of the problem. I also can't remember what ends up happening to the Lagrangian of an extended body.
Attached is a picture of the system.Thank you for any help!

 

[kuruman]

How many generalized coordinates do you need to specify the position of the rod unambiguously? What are they? Once you decide on these, then you need to write the Lagrangian in terms of them. Maybe you have done that but the itex code is messed up and I cannot read your equations.

 

[jncarter]

Yah, sorry about that. I didn't know that you can't have formatting commands in with the itex. Better now?

Right now I am using $\theta$ as my generalized coordinate, where $\theta$ is the angle of the center of mass from the center of the circle (the origin). Please look at the attached picture.

 

[kuruman]

Better now, thanks. Your potential energy in the Lagrangian term is almost OK. What is your reference point of the potential energy? If it is the center of the circle, then it is correct that U = - mg cosθ. However, L = T-U, so ...

Now for the kinetic energy term T. This is rotational motion of an extended body about the center of the circle. The kinetic energy then is (1/2)I(θ-dot)² where I is the moment of inertia of the rod about the center of the circle. So T = ...

 

[jncarter]

This may well be true, but we haven't gone over moments yet in class. I have done so in my undergraduate studies, but I would assume the professor wouldn't give us a problem with it at this point. Also, how would I calculate the moment? Could I just consider it two point masses, each located at |$\frac{l}{2}$| and add them up?

 

[kuruman]

This may well be true, but we haven't gone over moments yet in class.

This doesn't mean that you do not have to use them if needed.

I have done so in my undergraduate studies, but I would assume the professor wouldn't give us a problem with it at this point.

I don't want to second guess your professor, but I can't imagine that he/she would expect you to handle Lagrangians (normally covered at the junior-senior level) without expecting you to handle moments of inertia (normally covered in freshman physics).

Also, how would I calculate the moment? Could I just consider it two point masses, each located at |$\frac{l}{2}$| and add them up?

No. You would have to find (or look up) the moment of inertia of a rod about its center of mass, then apply the parallel axis theorem as explained here

http://hyperphysics.phy-astr.gsu.edu/hbase/parax.html

 

[mpw212002]

I am also working on this problem except i have the added fun of finding $\omega$ for the small departures from equilibrium.

I have found;

L = mlr$^{2}$$\dot{\theta}$$^{2}$ + Ir$^{2}\dot{\theta}$$^{2}$ - 2mlgrcos$\theta$

does this seem right for a lagrangian?

 

[vela]

I am also working on this problem except i have the added fun of finding $\omega$ for the small departures from equilibrium.

I have found;

L = mlr$^{2}$$\dot{\theta}$$^{2}$ + Ir$^{2}\dot{\theta}$$^{2}$ - 2mlgrcos$\theta$

does this seem right for a lagrangian?

No, the units don't work out at all for every term in your Lagrangian.

 

[jncarter]

I am also working on this problem except i have the added fun of finding $\omega$ for the small departures from equilibrium.

I have found;

L = mlr$^{2}$$\dot{\theta}$$^{2}$ + Ir$^{2}\dot{\theta}$$^{2}$ - 2mlgrcos$\theta$

does this seem right for a lagrangian?

I think we're in the same class. Caticha?

The problem with your lagrangian is that you have too many terms with units of length (l*r² in your T term and l*r in the U). Then there is the problem of actually finding the moment. I just can't understand how it comes into things. The two ends of the rod are not rotating about the CM, this isn't a seesaw motion, it's an extended pendulum. Maybe I need to re-draw the picture.