- #1
asd1249jf
The sum of 1-2+3-4+5..., and divergence
The sum of 1-2+3-4+5..., which can be written as
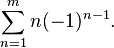
Diverges for m = infinity, yet there are postulates that this is equal to [tex]\frac{1}{4}[/tex].
First, I don't understand how you can obtain a fraction out of a natural numbers if they are consecutively added, regardless of if the number is positive or negative.
Second, I don't understand how this is equal to 1/4, when the infinite series diverges. Can anyone help me understand this postulate?
The sum of 1-2+3-4+5..., which can be written as
Diverges for m = infinity, yet there are postulates that this is equal to [tex]\frac{1}{4}[/tex].
First, I don't understand how you can obtain a fraction out of a natural numbers if they are consecutively added, regardless of if the number is positive or negative.
Second, I don't understand how this is equal to 1/4, when the infinite series diverges. Can anyone help me understand this postulate?