- #1
elegysix
- 406
- 15
I've been wondering how to calculate the area of intersection of two overlapping circles in terms of their radii. There's two cases I'm interested in:
The easier case:
Suppose there are two circles of radius R and r (R > r). The center of the larger circle is at the origin, and the center of the other circle is at (x,y)=(R,0). How can I find the area of the overlap in terms of R and r? I can't think of any clear way to do this by hand.
The more complicated case:
Do the same except let the center of the smaller circle lie between (R-r,0) < (x,y) < (R+r,0)
I've attached a drawing to help show the problem.
Thanks for any insight. This isn't for school, so there's no rush or anything. Just curious.
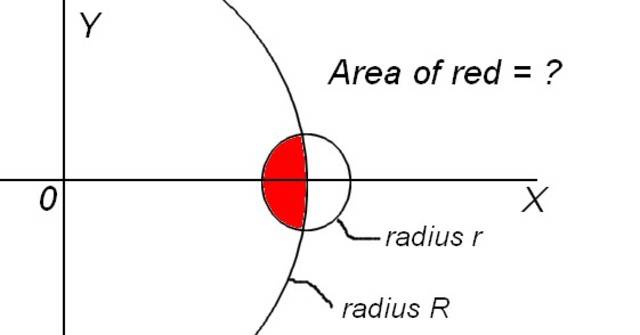
The easier case:
Suppose there are two circles of radius R and r (R > r). The center of the larger circle is at the origin, and the center of the other circle is at (x,y)=(R,0). How can I find the area of the overlap in terms of R and r? I can't think of any clear way to do this by hand.
The more complicated case:
Do the same except let the center of the smaller circle lie between (R-r,0) < (x,y) < (R+r,0)
I've attached a drawing to help show the problem.
Thanks for any insight. This isn't for school, so there's no rush or anything. Just curious.