Absolute Extrema and Relative Extrema?

[G01]

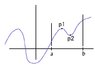
The extreme value theorem says that if a function is continuous on a closed interval then there are an absolute max and min on that interval. This means that the function can only be defined on this interval because if it existed outside this interval then the absolute extrema on the interval would just be relative extrema. Am I right here or a little confused?

Second Question:

Relative extrema are found on open intervals made from part of a bigger function right? This means that the function must exist outside the interval because the extrema are relative. Again, am I right hear or just confused.

Tanks alot

 

[Pengwuino]

Sounds near text-book for the first part

Not very sure about the 2nd part though.

 

[G01]

thanks alot, anyone got an idea for the second part?

 

[James R]

Looks ok to me.

 

[aliendoom]

Can someone explain the replies to me. Intuitively, the op's statements strike me as being wrong. It seems to me that just because there is an absolute max and an absolute minimum on some interval, that doesn't mean a function can't be defined outside that interval--as well as have higher or lower points outside the interval. When you are examining a function over an interval and talking about absolute min's and max's over that interval, that doesn't say anything about what happens outside the interval, does it? In the graph below, over the interval [a,b], p1 is a relative max, p2 is relative min, the absolute min occurs at a, and the absolute max occurs at b. However, outside the interval [a,b], the function has a higher max and a lower min.As for the second queston, it seems to me an interval can have relative maxes and mins as well as an absolute max and min--regardless of what is happening outside the interval. Also, what is the significance of the op's question changing from "closed interval" in the first question to "open interval" in the second question.

Thanks.

 

[HallsofIvy]

The first statement is false.
Consider an odd function f(x) such that f(0)= 0, rises to a maximum value of 1 at x= 1 (f(1)= 1) then has descends back toward 0 as x goes to infinity. Since f is odd, it descends to a minimum value of -1 at x= -1 (f(-1)= -1) then increases back toward 0 as x goes to negative infinity.
That function has 1 as absolute maximum, -1 as absolute minimum on any interval containing [-1, 1], including all x.
Perhaps even simpler: f(x)= sin(x) has 1 and -1 as absolute maximum and minimum on the entire real number line.

The theorem you are stating says that to guarantee that a (continuous) function takes on both maximum and minimum values on an interval the interval must be closed and bounded (i.e. compact, for those who know what that means.) That is a sufficient condition, not necessary.

As far as the second question is concerned, you have to be careful how you interpret it! Certainly a function that is defined only on a closed, bounded interval can have relative max and min on that interval. If you meant to say a continuous function having relative max and min must be defined only on an open interval you are wrong. Take, for example, the interval to be [-1, 1]. f(-1)= -1, draw f increasing then when f(x) is near 0, put a few "wiggles" in the graph, sort of like a sin curve but only going down to, say f(x)= -0.1 and up to 0.1. Finally, draw the curve up to f(1)= 1. That function is defined only on [-1, 1] and has as many relative max and min as you put wiggles in the graph. Of course, it also has a absolute max at 1 and a global min at -1. Any continuous function on a closed and bounded interval must have absolute max and min on that interval. If you meant to say that for a continuous function to have only relative max and min on a bounded interval then it must be open, that's true.

 

[aliendoom]

If you meant to say that for a continuous function to have only relative max and min on a bounded interval then it must be open, that's true.

Why is that?

 

[G01]

Thanks a lot everyone. Still a tiny bit confused on this topic though. Let's say we have the parabola y=x^2. Let's bound it on the interval [1,3] Now in my calc book, (Stewart 5e), the extreme value theorem is written something like this if I recall, If a function is bounded on a closed interval, it attains an ABSOLUTE max and and ABSOLUTE min somewhere on that interval. The book defines an absolute max as a number f(c) > all f(x) in the domain of f. Now the domain of f is (-infinity to infinity) in the case of y=x^2, Now back to the extreme value theorem, which was if a function is bounded on a closed interval, it has an absolute max and an absolute min on that interval. But in my case the absolute min is outside that interval and x=0. Am I just reading the theorem wrong, or is the wording of it funny in my book, because if its not it seems to my that the absolute max and mins on the closed interval are just relative max and mins? Thanks for putting up with me lol!

 

[hypermorphism]

Thanks a lot everyone. Still a tiny bit confused on this topic though. Let's say we have the parabola y=x^2. Let's bound it on the interval [1,3] Now in my calc book, (Stewart 5e), the extreme value theorem is written something like this if I recall, If a function is bounded on a closed interval, it attains an ABSOLUTE max and and ABSOLUTE min somewhere on that interval. The book defines an absolute max as a number f(c) > all f(x) in the domain of f. Now the domain of f is (-infinity to infinity)...

No, when one says "the function f on the interval blah", one is prescribing the domain of f to be "the interval blah". The extreme value theorem talks about a function on a closed interval.
Take some function in the plane, y=f(x). It says if you can put a rectangle around some portion of the graph of f, so that the portion within the rectangle doesn't exit the rectangle vertically, then inside that rectangle, f hits some maximal and some minimal value (if not at a relative extremum, then at least at the vertical edges of the rectangle). If you draw it out, there really doesn't seem to be any way for any other result to happen, but it remains necessary to prove the result always happens for all f and any closed interval.

 

[HallsofIvy]

Thanks a lot everyone. Still a tiny bit confused on this topic though. Let's say we have the parabola y=x^2. Let's bound it on the interval [1,3] Now in my calc book, (Stewart 5e), the extreme value theorem is written something like this if I recall, If a function is bounded on a closed interval, it attains an ABSOLUTE max and and ABSOLUTE min somewhere on that interval. The book defines an absolute max as a number f(c) > all f(x) in the domain of f. Now the domain of f is (-infinity to infinity) in the case of y=x^2, Now back to the extreme value theorem, which was if a function is bounded on a closed interval, it has an absolute max and an absolute min on that interval. But in my case the absolute min is outside that interval and x=0. Am I just reading the theorem wrong, or is the wording of it funny in my book, because if its not it seems to my that the absolute max and mins on the closed interval are just relative max and mins? Thanks for putting up with me lol!

Yes, you are reading the theorem wrong! The theorem in its most general form says that a continuous function maps a compact interval onto a a compact interval. In the real numbers, closed and bounded sets are compact (and vice-versa) so any closed and bounded interval is mapped onto a closed and bounded interval. Since the interval is bounded it has a least upper bound and an greatest lower bound. Since the interval is closed they will actually be in the set and so max and min values.

When you are looking at y= x², on the interval [1, 3], the fact that x² has a global minimum at x= 0 is irrelevant. when x= 1,
y(1)= 1 which is the smallest value y takes on on that interval. That is what "absolute minimum" means here: it is the the largest value the function takes on ON THAT INTERVAL.
By the way, the absolute maximum on the interval is at x= 3: y(3)= 9.

 

[G01]

THANK YOU IVY! That clears up alot. Am I right then, when I say that a relative extrema is any "peak or valley" in the function (where f`(x)=0). At these points f(x) will be greater than at any point NEAR it, hence the name relative. Absolute extrema then, are the highest or lowest value over the whole interval where the function is defined. And if we define a function over a closed interval, then the absolute max and min can be the endpoints or also the relative extrema contained in that interval

Am I making more sense now

 

[hypermorphism]

...
Am I right then, when I say that a relative extrema is any "peak or valley" in the function (where f`(x)=0). At these points f(x) will be greater than at any point NEAR it, hence the name relative. Absolute extrema then, are the highest or lowest value over the whole interval where the function is defined. And if we define a function over a closed interval, then the absolute max and min can be the endpoints or also the relative extrema contained in that interval
...

That's pretty much it.