- #1
boeing_737
- 12
- 0
Hi,
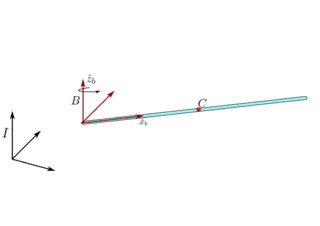
I am having a little bit of conceptual trouble with this problem and would appreciate your help. The problem setup is given in the figure. Let's say we have a slender uniform rigid arm(mass m, length l) in space, with a coordinate system [itex]B[/itex] attached to the left end of the arm as shown. C is the center of mass of the arm. We have a moment [itex]M_{z_b}[/itex] acting about the [itex]\hat{z}_{b}[/itex] axis.
Let [itex](u,v,w)[/itex] and [itex](p,q,r)[/itex] be the inertial velocity and inertial angular velocity vectors expressed in [itex]B[/itex]. I get the scalar equations of motion as (assuming that the angular velocity is only along [itex]\hat{z}_b[/itex]):
[itex]m \dot{u} - \frac{ml}{2} r^2 = F_{x_b}[/itex]
[itex]m \dot{v} + \frac{ml}{2} \dot{r} = F_{y_b}[/itex]
[itex]m \dot{w} = F_{z_b}[/itex]
[itex]0 = M_{x_b}[/itex]
[itex]-\frac{ml}{2} \dot{w} = M_{y_b}[/itex]
[itex]\frac{ml^2}{3} \dot{r} + \frac{ml}{2} \dot{v} = M_{z_b}[/itex]
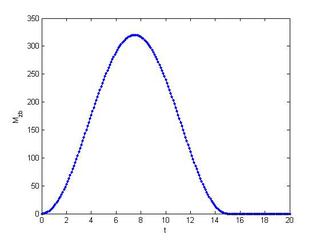
The applied moment is given as : [itex]M_{z_b}(t) = 160 \left(1 - \cos \left(\frac{2 \pi t}{15} \right) \right)[/itex]. For [itex]t > 15, M_{z_b} = 0[/itex]. See figure below :
Integrating these equations using MATLAB's ode45, I get the following plot :
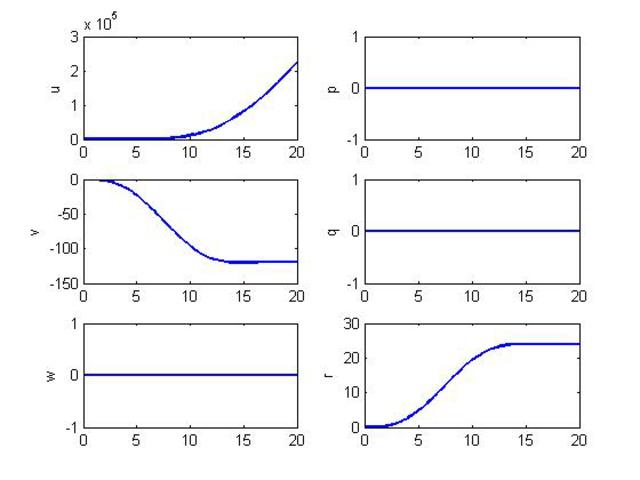
From the above figure :
1) There is only one component of angular velocity (yaw rate) which is as expected. But is the magnitude correct (ie should it reach 24 rad/s)?
2) I am not able to figure out what's going on with u. Why is it increasing so rapidly?
Any help would be really appreciated.
yogesh
I am having a little bit of conceptual trouble with this problem and would appreciate your help. The problem setup is given in the figure. Let's say we have a slender uniform rigid arm(mass m, length l) in space, with a coordinate system [itex]B[/itex] attached to the left end of the arm as shown. C is the center of mass of the arm. We have a moment [itex]M_{z_b}[/itex] acting about the [itex]\hat{z}_{b}[/itex] axis.
Let [itex](u,v,w)[/itex] and [itex](p,q,r)[/itex] be the inertial velocity and inertial angular velocity vectors expressed in [itex]B[/itex]. I get the scalar equations of motion as (assuming that the angular velocity is only along [itex]\hat{z}_b[/itex]):
[itex]m \dot{u} - \frac{ml}{2} r^2 = F_{x_b}[/itex]
[itex]m \dot{v} + \frac{ml}{2} \dot{r} = F_{y_b}[/itex]
[itex]m \dot{w} = F_{z_b}[/itex]
[itex]0 = M_{x_b}[/itex]
[itex]-\frac{ml}{2} \dot{w} = M_{y_b}[/itex]
[itex]\frac{ml^2}{3} \dot{r} + \frac{ml}{2} \dot{v} = M_{z_b}[/itex]
The applied moment is given as : [itex]M_{z_b}(t) = 160 \left(1 - \cos \left(\frac{2 \pi t}{15} \right) \right)[/itex]. For [itex]t > 15, M_{z_b} = 0[/itex]. See figure below :
Integrating these equations using MATLAB's ode45, I get the following plot :
From the above figure :
1) There is only one component of angular velocity (yaw rate) which is as expected. But is the magnitude correct (ie should it reach 24 rad/s)?
2) I am not able to figure out what's going on with u. Why is it increasing so rapidly?
Any help would be really appreciated.
yogesh
Last edited: