- #1
bob1182006
- 492
- 1
Homework Statement
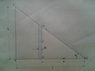
Find the Moment of Inertia for a uniformly cut wedge of Length L and mass M.
Rotated about an axis perpendicular to the tip of the wedge. so it increases in height and mass as you go -> L from 0.
Homework Equations
[tex]dI=r^2 dm=\rho r^2 dV=\rho r^2 A dr[/tex]
[tex]\rho = \frac{M}{V}[/tex]
The Attempt at a Solution
I just can't figure out how to setup the intergral. or any of the Moment of Inertial Integrals for that matter..
If I cut the wedge into vertical slices I get 1 small triangle at the tip, and then you'd get rectangles with some small triangle at the top of them.
Do I need to do this using 3/2 integrals? Or is it possible to do it with just 1? Because so far I only have knowledge of up to 1 integral :/.
Last edited: