- #1
Trenthan
- 54
- 0
Ey guys, this is a problem from my Mech Eng Dynamcis of Machine class
I believe i have the solution already since I've spoken to the lecture'r/tutors who run the subject but would like further clarification just incase I've done something completely wrong.
This is the problem
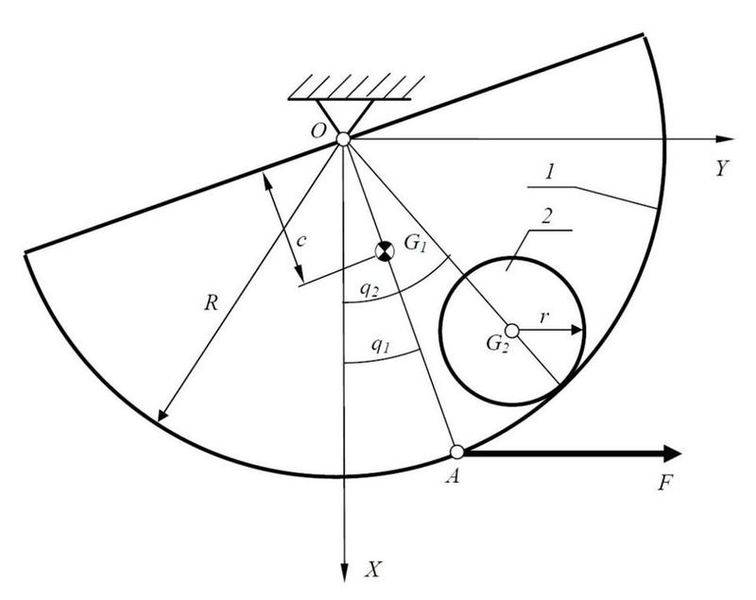
The semi cylindrical shell 1 is free to rotate about the horizontal axis Z of the inertial
system of coordinates XYZ. Its mass is M and its mass moment of inertia about the axis Z
is I1. The distance c locates its centre of gravity G1. The instantaneous position of the
shell is defined by the independent generalised coordinate q1. The cylinder 2 can roll over
the cylindrical shell without slipping. Mass of the cylinder is m and the mass moment of
inertia about its axis of symmetry is I2. The instantaneous position of the cylinder is
defined by the independent generalised coordinate q2. There is a constant and horizontal
force F applied to the shell at the point A.
a) the expression for the kinetic energy function of the system
I can easily do this, well generally can. However the slipe part is where I am struggling.
Basics first, SIMPLE case where the shell does NOT MOVE
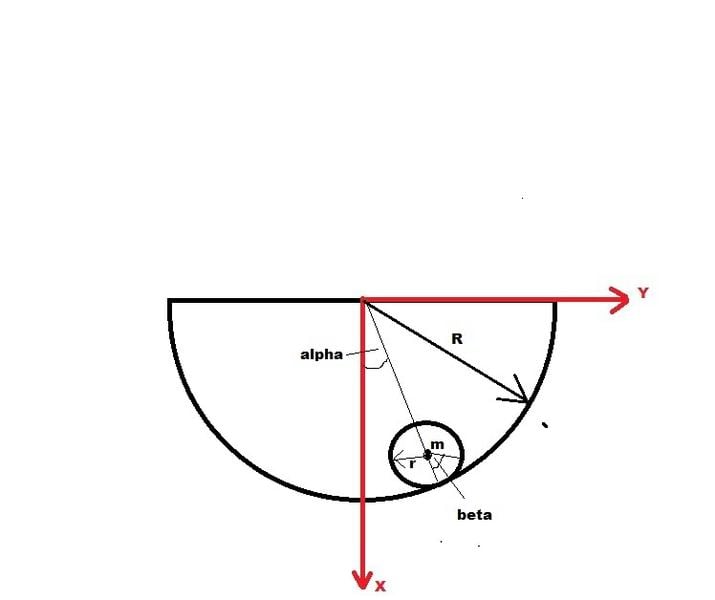
[tex]
\beta r = \alpha R
[/tex]
[tex]
\beta = \alpha \frac{R}{r}
[/tex]
[tex]
\dot{\beta} = \dot{\alpha} \frac{R}{r}
[/tex]
Now we have the above relation between angular velocity of the cylinder and its centre of mass with respect to the stationary shell.
Now here is where it gets weird for me
From what i understood, the absolut velocity of the cylinder is
[tex]
\omega= \dot{\beta} - \dot{\alpha}
[/tex]
Now when talking with the lecture'r he said you can think of it as
"the distance the cylinder rolls, minus curvature..., this is because the distance a cylinder rolls on a flat surface is a different length to the amount it does in an arc"
I understand the logic here, just not the above relation! If anyone can shed some light of where it comes from... please and thanks
Now jumping back to the main question
Using the same logic, and after speaking with him again
[tex]
\beta r = (q_{2}-q_{1}) R
[/tex]
[tex]
\beta = ( \dot{q_{2}} - \dot{q_{1}} ) \frac{R}{r}
[/tex]
Taking into account Curvature again, gives absolute angular velocity
[tex]
\omega = ( \dot{q_{2}} - \dot{q_{1}} ) \frac{R}{r} - \dot{q_{2}}
[/tex]
Now this i simply sub in as w in my kinetic energy equation
[tex]
T_{2} = \frac{1}{2} m r_{G2}^{2} + \frac{1}{2} \omega I \omega
[/tex]
(G2 is the Centre of Mass of the cylinder, & T2 is the kinetic energy of the cylinder, NOT the system**)
Im not sure what I've done in the last bit is correct. Seems very iffy to me.
-The " minus curvature" and also the "q2 - q1 i don't like.
The "q2 - q1" looks to me like I am only considering teh cylinder rolls the angle between the COM of the cylinder and the COM of the shell
After speaking with the tutor he did say there will be a relative component. I am not sure what i used is right though...
Any ideas guys?
Any help is appreciated guys, even if its to clarify what i have done. Or tell me the whole thnig is wrong and help point me in the right direction.
Cheers Trent, and thanks in advance
I believe i have the solution already since I've spoken to the lecture'r/tutors who run the subject but would like further clarification just incase I've done something completely wrong.
This is the problem
The semi cylindrical shell 1 is free to rotate about the horizontal axis Z of the inertial
system of coordinates XYZ. Its mass is M and its mass moment of inertia about the axis Z
is I1. The distance c locates its centre of gravity G1. The instantaneous position of the
shell is defined by the independent generalised coordinate q1. The cylinder 2 can roll over
the cylindrical shell without slipping. Mass of the cylinder is m and the mass moment of
inertia about its axis of symmetry is I2. The instantaneous position of the cylinder is
defined by the independent generalised coordinate q2. There is a constant and horizontal
force F applied to the shell at the point A.
a) the expression for the kinetic energy function of the system
I can easily do this, well generally can. However the slipe part is where I am struggling.
Basics first, SIMPLE case where the shell does NOT MOVE
[tex]
\beta r = \alpha R
[/tex]
[tex]
\beta = \alpha \frac{R}{r}
[/tex]
[tex]
\dot{\beta} = \dot{\alpha} \frac{R}{r}
[/tex]
Now we have the above relation between angular velocity of the cylinder and its centre of mass with respect to the stationary shell.
Now here is where it gets weird for me
From what i understood, the absolut velocity of the cylinder is
[tex]
\omega= \dot{\beta} - \dot{\alpha}
[/tex]
Now when talking with the lecture'r he said you can think of it as
"the distance the cylinder rolls, minus curvature..., this is because the distance a cylinder rolls on a flat surface is a different length to the amount it does in an arc"
I understand the logic here, just not the above relation! If anyone can shed some light of where it comes from... please and thanks
Now jumping back to the main question
Using the same logic, and after speaking with him again
[tex]
\beta r = (q_{2}-q_{1}) R
[/tex]
[tex]
\beta = ( \dot{q_{2}} - \dot{q_{1}} ) \frac{R}{r}
[/tex]
Taking into account Curvature again, gives absolute angular velocity
[tex]
\omega = ( \dot{q_{2}} - \dot{q_{1}} ) \frac{R}{r} - \dot{q_{2}}
[/tex]
Now this i simply sub in as w in my kinetic energy equation
[tex]
T_{2} = \frac{1}{2} m r_{G2}^{2} + \frac{1}{2} \omega I \omega
[/tex]
(G2 is the Centre of Mass of the cylinder, & T2 is the kinetic energy of the cylinder, NOT the system**)
Im not sure what I've done in the last bit is correct. Seems very iffy to me.
-The " minus curvature" and also the "q2 - q1 i don't like.
The "q2 - q1" looks to me like I am only considering teh cylinder rolls the angle between the COM of the cylinder and the COM of the shell
After speaking with the tutor he did say there will be a relative component. I am not sure what i used is right though...
Any ideas guys?
Any help is appreciated guys, even if its to clarify what i have done. Or tell me the whole thnig is wrong and help point me in the right direction.
Cheers Trent, and thanks in advance