- #1
alaam2005
- 5
- 0
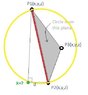
I would like to find a 3D coordinate of a point (X) on a circle, knowing two points on the circle (P1,P2) which represent the circle diameter and another point (P3) NOT on the circle but on its plane. Also known the length of the line from P2 to X, for example d. Another thing that may help, the line from the point P1 to X is perpindicular to the line X to P2.
Declared figure is attached.
Any help is appreciated.
Declared figure is attached.
Any help is appreciated.