- #1
DivergentSpectrum
- 149
- 15
So, a while back i read about this idea, but i can't find it anymore, so i was wondering if anybody else knows about it. here it is:
We know that if a vector field is conservative, then there exists some surface whos level curves are perpendicular to the vector field. or inversely, that the vector field grad(f) is pointing in the direction of highest increase of f.
Heres the shocker: unlike what you were told, even if a vector field is non conservative there still is some surface that cooresponds to it.
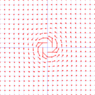
I attached some pictures, one of an obviously non-conservative vector field (see the rotation?)
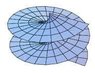
and one of a surface.
It seems to me, that the vector field shown is pointing in the direction of the highest increase of the surface given by the function z(x,y) . (note that these arent exact representations, they are just some pics i pulled off of google image search.)
I also realize, that the potential "function" shown isn't actually a function at all, according to my high school algebra teacher. The surface keeps spiraling around the z axis so there are multiple values for z at each point x and y. This isn't unheard of, for example sqrt(1)=1 and -1, so there should be some way to work around it.
I know all i really have here is a visual/intuitive argument, and maybe it is just an optical illusion, but I am really starting to think that a non conservative vector field may be the gradient of a multi-valued function. Who else knows about this? what does it mean? Does it have any applications(ie maxwells laws for magnetism)?
We know that if a vector field is conservative, then there exists some surface whos level curves are perpendicular to the vector field. or inversely, that the vector field grad(f) is pointing in the direction of highest increase of f.
Heres the shocker: unlike what you were told, even if a vector field is non conservative there still is some surface that cooresponds to it.
I attached some pictures, one of an obviously non-conservative vector field (see the rotation?)
and one of a surface.
It seems to me, that the vector field shown is pointing in the direction of the highest increase of the surface given by the function z(x,y) . (note that these arent exact representations, they are just some pics i pulled off of google image search.)
I also realize, that the potential "function" shown isn't actually a function at all, according to my high school algebra teacher. The surface keeps spiraling around the z axis so there are multiple values for z at each point x and y. This isn't unheard of, for example sqrt(1)=1 and -1, so there should be some way to work around it.
I know all i really have here is a visual/intuitive argument, and maybe it is just an optical illusion, but I am really starting to think that a non conservative vector field may be the gradient of a multi-valued function. Who else knows about this? what does it mean? Does it have any applications(ie maxwells laws for magnetism)?
Attachments
Last edited: