2-d mass-spring-damping system

[pure72]

Homework Statement

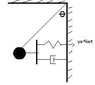
determine the equations of motion for the attached 2-d system.

ball of mass m
wire with negligible mass
spring with sping constant k
dashpot with damping coefficient c
displacement function of y=y*e^(iwt)
theta is the initial angle of displacement

Homework Equations

only mass to be considered is mass of ball
never seen this type of question before , not sure
can someone recommend a textbook that would help with this problem? have youseen this question before??

thx

 

[flatmaster]

A few questions to clairify...

Are the mass, spring and damper all connected? Your diagram is ambiguious.
Are you allowed to assume small angles for the pendulum?
Is the spring driven with y=y*e^(iwt)?

If so, seek steady state solutions for a SHO of the same frequency as your driving frequency. You should have a family of solutions y=An*e^(i*2*Pi*n*wt). You then can determine your An's by satisfying your initial condition.

 

[pure72]

the spring and damper attach to a plate or bar of negligible mass.
the plate attaches to the mass by a rigid wire of negligible mass.
you can assume small swings for the pendulum, and/or small angle approximation.
the displacement function might be used as follows:

Force = -kx = -k(x-y) = -kx + k*Y*e^(iwt) , similarly it would affect the damper.

not sure what you mean by An, is this an expression for the amplitude?
I want to find Newtons equations of motion with terms that involve the derivatives of x.

thx

 

[flatmaster]

Yeah, that's the idea. You make your second degree diff eq., then solve for position as a function of time. The An's are indeed amplitudes. The reason you guess that solution is because after a long period of time, the oscilator will always oscilate at the frequency at witch you are driving it. Thus, the angular frequency "w" that you guess in the solution is the same angular frequency that is driving the spring. However, I get ahead of myself, Let's just settle on the sum of forces first.

 

[flatmaster]

I agree with your time-dependent equation for the spring force. I assume capital Y is the term for the magnitude of the spring's oscilation.

 

[flatmaster]

Now for the force from the pendulum, I assume you know the leingth L. Small angle approx says x/L = cos(theta) = tan(theta). THei leads to.

F= mgx/L

Sum of all F = Fp + Fs + Fd

'' = mgx/L + kx + kYe^(iwt) - c(dx/dt)

I make damping term negative to keep constant c positive. Rearanging to see the DE better...

x'' = gx + kYe^(iwt) - c x'

Where primes indicate time derivatives and g = (mgx/L) + k

 

[flatmaster]

Agree so far?

 

[pure72]

I think the force of the damper should be Fd = -c(x'-y') = -c(x') + Y*c*i*w*e^(iwt)

not sure about the small angle approximation, where can I find it online?

thx

 

[flatmaster]

.../|
L / | aprox. L
../ |
/__|
x

Because you can assume the angle theta is small, you can assume the actual change in height of the bob is neglagable. Thus Sin(theta)= Tan(theta)

 

[pure72]

what do you think about this eqn:

sum forces x: m(x'')= m*g*cos(theta) -c(x') + Y*c*i*w*e^(iwt) -kx + k*Y*e^(iwt)
where cos(theta) = 1 (small angle)
so,

m(x'')= m*g -c(x') + Y*c*i*w*e^(iwt) -kx + k*Y*e^(iwt)

what types of things can I do once I have the equation of motion

thx

 

[flatmaster]

Looks like you forgot one of the spring terms (+kx). Also, that Approximation for theta removes too much information. You removed all dependenct on theta.

Here's the pendulum force more explicitly.

The vertical part of tension must cancel force of gravity.
TCos(theta) =mg

T = mg/Cos(theta)

However, the restoring force important in the problem is the x component of the tension

Tx = TSin(theta) = mg (Sin(theta)/Cos(theta))

Tx = mg Tan(theta)
Because theta is small, Tan(theta) = Cos(theta)

(maby sketch out a right triangle with a small angle to convince yourself of this point. The leingth of the hypotoneuse is nearly equal to the leingth of the side adjacent to the small angle. )

Tx = mg Cos(theta)
Cos(theta) = x/l

Tx = mgx/l

And this is the linear restoring force that would lead to a SHO for a pendulum.

 

[pure72]

I think you can get theta back by taking moments about some point and getting an angular acceleration.

I don't have anymore time to work on this problem though, it was for prepartion of an exam..

thank you for the help though I might look over the problem again later if I get time.

 

[Dr.D]

You really should ask your instructor to show you his protractor that measures complex angles. The angle e^(iwt) is definitely complex. This is a poorly stated problem, even if we know what was intended.