- #1
dbconfession
- 14
- 0
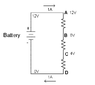
Please bear with me as I'm relatively new to hands-on circuitry. I have a breadboard powered by a 9V alkaline battery. If I hook up an LED to the positive strip and ground to the negative strip, the circuit completes and the bulb lights.
If, however, I take a simple 22 AWG wire to jump from pos to negative anywhere in the circuit, the bulb cuts out. I figured I'm missing something fundamental about electron flow and that you can't run two bridged items. But then Instead of using the jumper, I used a voltmeter to read the voltage of the circuit created by the bulb. This time the bulb stayed on and the volt-meter read just fine. Again, i ran a simple jumper from pos to neg. Sure enough once again the circuit was broken; the meter dropped to zero and the bulb went out. If I remove just one end of the jumper, the circuit closes again and power is restored.
What is happening here? There is no such thing as too much detail. As much as possible please so that I understand physically what is happening to my circuit. Thanks in advance.
If, however, I take a simple 22 AWG wire to jump from pos to negative anywhere in the circuit, the bulb cuts out. I figured I'm missing something fundamental about electron flow and that you can't run two bridged items. But then Instead of using the jumper, I used a voltmeter to read the voltage of the circuit created by the bulb. This time the bulb stayed on and the volt-meter read just fine. Again, i ran a simple jumper from pos to neg. Sure enough once again the circuit was broken; the meter dropped to zero and the bulb went out. If I remove just one end of the jumper, the circuit closes again and power is restored.
What is happening here? There is no such thing as too much detail. As much as possible please so that I understand physically what is happening to my circuit. Thanks in advance.