Are Wormholes Physically Possible in Our Universe?

[ChrisVer]

Well I just have one question. Is the existence of wormholes really possible or not?
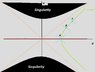
I've only seen them appearing in the Kruskal metric formalism, where we set the timelike parameter=0... However any motion on that "space" seems unphysical to me (it lies outside any possible light cone).

See attachment- no matter where I move the lightcone in region I, I cannot send anything to region III.

 

[PAllen]

Traversible (via timelike world lines) wormholes are possible only if you violate energy conditions. In my opinion (but it is hardly unversal), classical GR should be taken to encompass the dominant energy condition, which would preclude traversible wormholes. However, such basic quantum features as Hawking radiation violate all the the classical energy conditions, so this leaves the possibility of traversible wormholes as an open question.

[I see George Jones cross posted with me. Fortunately, our posts are consistent.]

 

[George Jones]

There are many other wormhole solutions for which the wormholes are traversable by timelike curves.

The theoretical possibility of the existence of such wormholes is an area of active research. Stable traversable wormholes, require "exotic" matter to hold them open, and exotic matter is such that some observers measure its density to be negative. There are some hints from quantum theory that exotic matter is theoretically possible, but not everyone agrees on how much is needed to hold a wormhole open, how much is possible, etc.

See

http://arxiv.org/abs/0710.4474

 

[ChrisVer]

Also , if possible, the whole Kruskal coordinates are lame... I have two problems about them:
1. Everything seems it comes from the infinite past to today (if it follows physical trajectories) from a singularity (in the graph the singularity below)... so it seems things could "move out" the swarchild radius, coming from it...
2. I cannot see how there can be closed trajectories for a particle... Everything seems to be falling into the singularity even at infinite time (if its velocity is equal to c)... the trajectories of constant radius in the Kruskal diagram are hyperbolas in the right region (r>r_s... this means that in order to follow circular motion, something would have to run faster than light... not only that, in fact every physical trajectory is doomed to fall in the singularity no matter how I choose it...
The only "orbit" I can "feel" is that of particles moving at c... exactly because their falling time is infinite.

 

[George Jones]

Also , if possible, the whole Kruskal coordinates are lame... I have two problems about them:
1. Everything seems it comes from the infinite past to today (if it follows physical trajectories) from a singularity (in the graph the singularity below)... so it seems things could "move out" the swarchild radius, coming from it...

The entirety of the extended Schwarzschild solution is not taken seriously as a physical spacetime.

2. I cannot see how there can be closed trajectories for a particle... Everything seems to be falling into the singularity even at infinite time (if its velocity is equal to c)... the trajectories of constant radius in the Kruskal diagram are hyperbolas in the right region (r>r_s... this means that in order to follow circular motion, something would have to run faster than light...

How so? On a Penrose diagram, these hyperbolae of constant r have slopes with magnitudes greater than one, and thus are timelike.

 

[ChrisVer]

How so? On a Penrose diagram, these hyperbolae of constant r have slopes with magnitudes greater than one, and thus are timelike.

I'll try to illustrate it with this diagram again...
We have the particle moving from A to B to C...
From that we see that going from A to B is pretty easy, within the light cone, keeping casuality...
Then we see that from B to C it becomes even more difficult to remain at r=const trajectory, it needs to move pretty fast...
keep going from C to any other event is even harder...
The only thing that can move on r=const is something which has speed c...
every other trajectory, no matter where you begin, due to casuality will leave region I and fall into region II (r<r_s) and the singularity...
Maybe my diagram is not so illustrative, since it's done by mouse and paint... But my idea is also based on geometry:
only a parallel line to the orange ones (r=r_s) doesn't have to intersect them - that means v=c... all others (non parallel) will eventually intersect it and fall into the real singularity of the Schwarchild's metric

 

[PAllen]

I'll try to illustrate it with this diagram again...
We have the particle moving from A to B to C...
From that we see that going from A to B is pretty easy, within the light cone, keeping casuality...
Then we see that from B to C it becomes even more difficult to remain at r=const trajectory, it needs to move pretty fast...
keep going from C to any other event is even harder...
The only thing that can move on r=const is something which has speed c...
every other trajectory, no matter where you begin, due to casuality will leave region I and fall into region II (r<r_s) and the singularity...
Maybe my diagram is not so illustrative, since it's done by mouse and paint... But my idea is also based on geometry:
only a parallel line to the orange ones (r=r_s) doesn't have to intersect them - that means v=c... all others (non parallel) will eventually intersect it and fall into the real singularity of the Schwarchild's metric

This is a problem with a picture rather than the math. A (timelike, exterior) hyperbola of constant r has constant proper acceleration (not increasing). It's position in relation to the timelike killing field of the geometry is constant. It is just equivalent to sitting on the surface of a planet.

 

[PeterDonis]

only a parallel line to the orange ones (r=r_s) doesn't have to intersect them - that means v=c... all others (non parallel) will eventually intersect it and fall into the real singularity of the Schwarchild's metric

Are you saying that the r = const hyperbola will eventually intersect the horizon (the straight line going up and to the right)? If so, that's obviously wrong. The horizon is an asymptote to the hyperbola, and no hyperbola can ever intersect its asymptote; that's what "asymptote" means.

 

[George Jones]

Another way to see it: for your hyperbola there is a constant $k$ with $k = u^2 - v^2$. Differentiating this equation with respect to $u$ gives

$$\frac{dv}{du} = \frac{u}{v}$$

for your hyperbola. Since $u < |v|$ for all events on your hyperbola, $| u /v | > 1$, and your hyperbola is always timelike.

$$\frac{dv}{du} = 1$$

(lightlike) only "happens at infinity", i.e., it doesn't actually happen.

 

[ChrisVer]

I am saying everything in order to keep casuality...
Just draw a light cone on the diagram... the only parallel line to that of r=r_s (45degrees in the diagram), is the light cone line (45 degrees)...
Every other trajectory lying within the lightcone (which keeps casuality, take for example 46 Degrees or any bigger angle) would have to intersect r=r_s and so your particle would eventually end in the singularity...instead of orbiting in constant or non-constant r (so that's why I made the statement that there can be no closed trajectories)

 

[PAllen]

I am saying everything in order to keep casuality...
Just draw a light cone on the diagram... the only parallel line to that of r=r_s (45degrees in the diagram), is the light cone line (45 degrees)...
Every other trajectory lying within the lightcone (which keeps casuality, take for example 46 Degrees or any bigger angle) would have to intersect r=r_s and so your particle would eventually end in the singularity...instead of orbiting in constant or non-constant r (so that's why I made the statement that there can be no closed trajectories)

That is no different than the statement that from any event on the world line of someone sitting on a planet, the free fall trajectories would include hitting the center of the earth. You are emphasizing a coordinate artifact. It 'looks' like the region of a light cone outside the horizon gets smaller and smaller. But, in fact, nothing changes at all (that is what it means to say the geometry is static). If you transform to the local frame of each point along a constant r hyperbola, the 'fraction' of infalling free fall trajectories versus escaping ones, versus orbiting ones, remains exactly constant.

 

[PeterDonis]

Every other trajectory lying within the lightcone (which keeps casuality, take for example 46 Degrees or any bigger angle) would have to intersect r=r_s

No, every *straight line* (i.e, geodesic) trajectory has to intersect r = r_s. The r = const trajectory is not a straight line (i.e., not a geodesic). It's a hyperbola. As George Jones and I have already shown you, that hyperbola never intersects its asymptote, even though it remains at a timelike slope (inside the local light cone) everywhere. Even in flat spacetime you can have hyperbolic trajectories that never intersect their asymptotes, which are light rays.

 

[WannabeNewton]

I am saying everything in order to keep casuality...
Just draw a light cone on the diagram... the only parallel line to that of r=r_s (45degrees in the diagram), is the light cone line (45 degrees)...
Every other trajectory lying within the lightcone (which keeps casuality, take for example 46 Degrees or any bigger angle) would have to intersect r=r_s and so your particle would eventually end in the singularity...instead of orbiting in constant or non-constant r (so that's why I made the statement that there can be no closed trajectories)

This is completely incorrect but I might know the source of your confusion. Don't forget that in curved space-times the light cones are local. When you solve for the light cones in Schwarzschild space-time, e.g. by setting the space-time interval to zero in the Kruskal coordinates with the local 2-spheres suppressed, you get two sets of intersecting curves (forming the light cones) depending on the Kruskal coordinates. This is just the explicit realization of the fact that in GR light cones are local. This means that a given time-like curve or world-line need only have its 4-velocity within the light cone at any given event, and not necessarily within the "really large light cone" in the Kruskal diagram that you see emanating from the origin of the coordinates. Of course for radial light cones the coordinate dependence simplifies greatly, in fact it becomes trivial and we just get the same radial light cone at each point in space-time but this doesn't change the fact that time-like curves need only have their 4-velocities at any given event lie within the radial light cone at that event; this is local causality.

This should make it clear that the $r = \text{const.}$ world-line is perfectly causal as it is evident from the diagram that at each event on this world-line, the tangent lies within the local light cone there, even for the (coordinate-wise) trivial radial light cones.

 

[ChrisVer]

Thanks for the statements, but I need to clarify it a little bit more...
For example you say that I can have light cones only locally, and while I move on the diagram, the cone lines might be distorted due to curved spacetime?
So let me try to see it through formulas...
$ds^{2}_{schwarz}= (1- \frac{r_{s}}{r}) dt^{2} - \frac{1}{(1- \frac{r_{s}}{r})} dr^{2} - r^{2} dθ^{2} - r^{2} sin^{2}θ dφ^{2}$
let's only care about the 1st two terms, since they are the ones who make the distinction between Kruskal and Schwarzschild metrics (the coord transformation connecting them, only involves $u,v$ with $t,r$).

$ds^{2}_{schwarz}= (1- \frac{r_{s}}{r}) dt^{2} - \frac{1}{(1- \frac{r_{s}}{r})} dr^{2}$
Asking for the lightcone, $ds^{2}=0$

$(1- \frac{r_{s}}{r}) dt^{2} = \frac{1}{(1- \frac{r_{s}}{r})} dr^{2}$

$\frac{dr}{dt}= \pm (1- \frac{r_{s}}{r})$

So in the Schwarchild diagram, the slope of a lightcone on the $(t,r)$ diagram is ~45deg straight line for large r's, and as we go closer to the schwarzschild's radius coordinate distances the slope becomes almost 0... So if I had to draw a light cone on that diagram from point to point I should change the slope of the lightcone lines?

The same statement (change of slope- not necessarily in the same way) you say should be true for the Kruskal diagram?

 

[PeterDonis]

So in the Schwarchild diagram, the slope of a lightcone on the $(t,r)$ diagram is ~45deg straight line for large r's, and as we go closer to the schwarzschild's radius coordinate distances the slope becomes almost 0... So if I had to draw a light cone on that diagram from point to point I should change the slope of the lightcone lines?

On the Schwarzschild diagram, yes.

The same statement (change of slope- not necessarily in the same way) you say should be true for the Kruskal diagram?

No. On the Kruskal diagram, the light cones are always at 45 degree angles. The reason the r = const line does not intersect the horizon is *not* because the light cone slopes change on the Kruskal diagram; they don't. The reason the r = const line does not intersect the horizon is, as has been pointed out several times now, that the r = const line is a hyperbola and the horizon is its asymptote.

 

[ChrisVer]

No. On the Kruskal diagram, the light cones are always at 45 degree angles. The reason the r = const line does not intersect the horizon is *not* because the light cone slopes change on the Kruskal diagram; they don't. The reason the r = const line does not intersect the horizon is, as has been pointed out several times now, that the r = const line is a hyperbola and the horizon is its asymptote.

The reason this has been stated many times, is because I don't understand how something moving on r=const hyperbola is not accelerating...
Probably I should focus more in understanding Pallen's post:

"That is no different than the statement that from any event on the world line of someone sitting on a planet, the free fall trajectories would include hitting the center of the earth. You are emphasizing a coordinate artifact. It 'looks' like the region of a light cone outside the horizon gets smaller and smaller. But, in fact, nothing changes at all (that is what it means to say the geometry is static). If you transform to the local frame of each point along a constant r hyperbola, the 'fraction' of infalling free fall trajectories versus escaping ones, versus orbiting ones, remains exactly constant."

Since that's the reason I am not getting it... If I should interpret it somehow, would you mind checking it?
So maybe it seems that the particle should keep accelerating from event to event, but that's not true, it's just keeps moving with the same velocity on r=const hyperbola... the misconception comes from looking the diagram and seeing it "approaching" the horizon while that's not the case... or in other words the "grids" within the lightcone are disformed from event to event... and although something seems to be accelerating to reach speed=c, what is happening is that the "velocities" in the light cone get more diverged?

 

[PeterDonis]

The reason this has been stated many times, is because I don't understand how something moving on r=const hyperbola is not accelerating...

It is accelerating. An object hovering at a constant altitude over a black hole (or any other gravitating body) has to accelerate to maintain its altitude. (Or it has to be pushed upward by something else; for example, when you're standing on the surface of the Earth, the Earth is pushing you up. That's why you feel weight; you're accelerating upwards.)

If you are thinking about objects in circular free-fall orbits around a black hole (or other gravitating body), the Kruskal diagram can't represent those; you need at least a 3-dimensional diagram (two space dimensions and one time dimension).

 

[ChrisVer]

Then...I think I am making circular statements at the moment... if it's to reach the light cone line by accelerating then the particle would have to reach c to reach the asymptote... otherwise it cannot move at r=const or any closed orbit...

http://i.stack.imgur.com/bYrq7.png

 

[WannabeNewton]

The same statement (change of slope- not necessarily in the same way) you say should be true for the Kruskal diagram?

For arbitrary light cones yes but those can't really be drawn on the usual Kruskal diagram since the 2-spheres are suppressed in Kruskal diagrams; as such, for the purposes of the Kruskal diagram, we stick to the much simpler case of radial light cones for which the light cones are the same at every event. But the point is that anyone light cone only exists at a given event. A light cone in curved space-time is the same as a light cone in SR at the origin of Minkowski space-time mapped isometrically into the tangent space at each event in the curved space-time. This means that when I want to draw a time-like curve on a diagram, all I have to do is make sure that its tangent vector lies within the light cone present at each event on the curve. As such, there is no reason for a time-like curve to necessarily intersect the horizon.

Consider the $r = \text{const.}$ curve for $r > 2M$. It is given by the conic section $U^2 - V^2 = \text{const.}$ and so $|\frac{dV}{dU}| = |\coth(\frac{t}{4M})| > 1$ which is the necessary and sufficient condition for the tangent vector to a curve to lie inside the radial light cone at a given event on the Kruskal diagram i.e. for the curve to be time-like.

 

[ChrisVer]

Do you have any reference where I could see the geodesic equations for the Kruskal metric?

 

[PeterDonis]

if it's to reach the light cone line by accelerating then the particle would have to reach c to reach the asymptote...

A particle moving on a timelike worldline can never "reach the light cone" in its local piece of spacetime, no matter how it accelerates. That's true in curved spacetime just as it is in flat spacetime.

otherwise it cannot move at r=const or any closed orbit...

http://i.stack.imgur.com/bYrq7.png

The image you give only includes the radial spatial dimension, so, as I said before, it can't even represent a closed free-fall orbit, which requires tangential motion. It can only represent worldlines whose only motion is radial. The r = const worldline is such a worldline. If you still don't understand how that worldline can keep on going forever without intersecting the horizon, I would recommend that you get clear on that first, before trying to understand anything else about the Kruskal diagram. First try the case of an object with constant proper acceleration in flat spacetime, whose trajectory on a standard Minkowski diagram is also a hyperbola, and also never intersects its Rindler horizon; the Rindler horizon is, in this respect, an exact analogue to the horizon of a black hole.

http://en.wikipedia.org/wiki/Rindler_coordinates#The_Rindler_horizon

 

[stevendaryl]

Something I don't understand about whether wormholes are physical or not is the relationship between topology and curvature.

Topology in 2D is what makes the difference between a plane versus a cylinder versus a sphere versus a torus. Topology is not determined by curvature; for example, a cylinder or torus have zero curvature, just like a plane. But I think it's true that some topologies are not consistent with certain curvatures--a sphere for instance cannot have zero curvature everywhere.

So getting back to wormholes. A wormhole is a topological feature of spacetime; it means that spacetime is not simply connected. What does that imply about curvature?

 

[George Jones]

Then...I think I am making circular statements at the moment... if it's to reach the light cone line by accelerating then the particle would have to reach c to reach the asymptote... otherwise it cannot move at r=const or any closed orbit...

http://i.stack.imgur.com/bYrq7.png

I think I finally get it. Yes, the r = const curves on Kruskal diagrams have non-zero 4-acceleration. If you want to consider geodesic circular orbits, you need to consider another (dimension) coordinate. Transforming to Krsukal coordinates involves (t, r, theta, phi) going to (u, v, theta, phi), i.e., theta and phi left alone.

If you want to consider a circular orbit, you can't just consider (t, r) and (u, v); at least one other coordinate must also come into play. For example, fix r = constant for the orbital radius and theta = pi/2 for the orbital plane, and let phi roam freely. Consequently, in Schwarzschild coodinates, dr = d theta = 0, but d phi is not zero.

For such orbits, it is possible (but not necessary) to have zero 4-acceleration.

 

[PeterDonis]

Topology is not determined by curvature; for example, a cylinder or torus have zero curvature, just like a plane.

It's even more "not determined" than that. You can have a manifold that is topologically a cylinder or a torus, but with nonzero intrinsic curvature. (In fact, the usual visualization of a topological torus--a doughnut--has nonzero intrinsic curvature.)

But I think it's true that some topologies are not consistent with certain curvatures--a sphere for instance cannot have zero curvature everywhere.

I think that's right, yes.

So getting back to wormholes. A wormhole is a topological feature of spacetime; it means that spacetime is not simply connected. What does that imply about curvature?

It depends on whether you're just talking about abstract math, or about physics. Mathematically, I don't know what the constraints are on curvature for non-simply-connected manifolds: a torus, for example, is not simply connected, but can have zero curvature.

Physically, a wormhole spacetime would have to be a solution of the EFE, and the only solution of the EFE with zero curvature everywhere is flat Minkowski spacetime. So any physical spacetime with wormholes present would have to have nonzero curvature.

 

[Bill_K]

But I think it's true that some topologies are not consistent with certain curvatures--a sphere for instance cannot have zero curvature everywhere.

Sounds like the Gauss-Bonnet Theorem.

 

[stevendaryl]

Physically, a wormhole spacetime would have to be a solution of the EFE, and the only solution of the EFE with zero curvature everywhere is flat Minkowski spacetime. So any physical spacetime with wormholes present would have to have nonzero curvature.

Are you sure about that? I would think that a cylindrical (or toroidal) universe would be consistent with the EFE. After all, as far as the field equations are concerned, there is no difference between a toroidal universe and one whose mass/energy density just happens to be periodic in space.

 

[PeterDonis]

Are you sure about that? I would think that a cylindrical (or toroidal) universe would be consistent with the EFE.

Hm, yes, you're right, since the EFE is local, it can't by itself constrain the global topology.

After all, as far as the field equations are concerned, there is no difference between a toroidal universe and one whose mass/energy density just happens to be periodic in space.

If the mass/energy density is nonzero, however, there must be curvature; that *is* required by the EFE. So yes, a given solution of the EFE could describe a toroidal (but non-flat) universe, or an infinite universe with periodic mass/energy density; but a toroidal vacuum universe (like a square region of Minkowski spacetime with boundaries identified) would still require zero stress-energy for the EFE to be satisfied.

 

[pervect]

Do you have any reference where I could see the geodesic equations for the Kruskal metric?

You can write down the geodesic equations directly from the metric by calculating the Christoffel symbols.

See for instance the general geodesic equation as described in http://ned.ipac.caltech.edu/level5/March01/Carroll3/Carroll3.html

This doesn't usually give a lot of insight though, the equations are messy. What gives more insight with less calculation is finding the Killing vectors.

See for instance http://ned.ipac.caltech.edu/level5/March01/Carroll3/Carroll7.html

The dot product of the any killing vector and the tangent vector of a geodesic is constant. So instead of a very messy nonlinear differential equation, you have a set of simple linear differential equation.

You can also add the requirement that the norm of the tangent vector be unity if the geodesic is parameterized by proper time (which is usually what you want0.

The only Killing vector that has a different form in the KS coordinates is $\partial / \partial t$. You can find some discussion of what this Killing vectors look like expressed in Kruskal coordinates at.

https://www.physicsforums.com/showthread.php?t=508703
https://www.physicsforums.com/showthread.php?t=395302

So if you follow the discussion of how to get the motion from the Killing vectors, and how to transform the Killing vectors to the new coordinates, you'll have the math to work out motions in KS coordinates.

However, the discussion already given to your problem is much easier to understand than the detailed math you'll need to work out motions in KS coordinates.

I'm not sure that the more advanced answer to your question will help you understand more, but just in case it does I'm giving it.

I think that re-reading the less technical answers already would be a much easier approach to understanding what's happening

 

[WannabeNewton]

So getting back to wormholes. A wormhole is a topological feature of spacetime; it means that spacetime is not simply connected. What does that imply about curvature?

Space-time having a non-trivial fundamental group does not imply the existence of a wormhole. It is a sufficient but not necessary condition. Furthermore the Einstein-Hilbert action does not contain any topological terms in it so it does not codify the topology in itself, an initial Cauchy surface must be provided and if the space-time is hyperbolic the Cauchy data can be evolved uniquely under Einstein's equations (think of it as a boundary value problem). That the Einstein-Hilbert action contains no topological terms is a feature of it being four dimensional; in two dimensions the same integral is entirely topological thanks to the Gauss-Bonnet theorem. One cannot easily relate the existence of non-trivial fundamental groups in Lorentzian 4-manifolds constrained to satisfy Einstein's equations to the Riemann or Ricci curvature of that manifold. .

 

[Bill_K]

Space-time having a non-trivial fundamental group does not imply the existence of a wormhole. It is a sufficient but not necessary condition.

Don't you mean necessary but not sufficient?

an initial Cauchy surface must be provided and if the space-time is hyperbolic the Cauchy data can be evolved uniquely under Einstein's equations (think of it as a boundary value problem).

What about a periodic spacetime, in which the hypersurface t = t0 has been identified with t = t0 + C? There's no guarantee that the data evolved from t0 will match the data that has already been determined at t0 + C.

 

[WannabeNewton]

Don't you mean necessary but not sufficient?

Sorry, yes.

What about a periodic spacetime, in which the hypersurface t = t0 has been identified with t = t0 + C? There's no guarantee that the data evolved from t0 will match the data that has already been determined at t0 + C.

My apologies but, while I don't disagree that such a situation can arise, I'm not seeing what point is being made exactly with regards to the quoted statement.

 

[Bill_K]

if the space-time is hyperbolic the Cauchy data can be evolved uniquely under Einstein's equations (think of it as a boundary value problem).

What about a periodic spacetime, in which the hypersurface t = t0 has been identified with t = t0 + C? There's no guarantee that the data evolved from t0 will match the data that has already been determined at t0 + C.

My apologies but, while I don't disagree that such a situation can arise, I'm not seeing what point is being made exactly with regards to the quoted statement.

For such a spacetime, the general Cauchy initial value problem fails to have a solution. Only for very specific values of the data will it be self-consistent. This is a mathematical statement, but with important physical consequences! It's exactly the reason that I can't kill my grandfather.

 

[WannabeNewton]

For such a spacetime, the general Cauchy initial value problem fails to have a solution. Only for very specific values of the data will it be self-consistent. This is a mathematical statement, but with important physical consequences!

Oh I see. I'll try to read more on that, thank you for pointing that out :)

It's exactly the reason that I can't kill my grandfather.

Well we wouldn't want that now would we!

 

[ChrisVer]

Don't you mean necessary but not sufficient?


What about a periodic spacetime, in which the hypersurface t = t0 has been identified with t = t0 + C? There's no guarantee that the data evolved from t0 will match the data that has already been determined at t0 + C.

would that mean you compactify time in a circle? then I guess due to periodicity you're driven to making your last statement true...

 

[PAllen]

For such a spacetime, the general Cauchy initial value problem fails to have a solution. Only for very specific values of the data will it be self-consistent. This is a mathematical statement, but with important physical consequences! It's exactly the reason that I can't kill my grandfather.

I thought the initial value formulation only produced globally hyperbolic manifolds, which would exclude such a solution. To get such a solution, I would think you need to pose additional topological constraints, which may or may not be consistent with initial conditions.