Geometry (circle inscribed into triangle)

[Inspector Gadget]

I'm working on this problem.

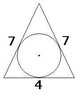
The only given information is the circle is inscribed into the triangle. And you have to find the radius of the circle.

The answer is...

$$\frac{2\sqrt{5}}{3}$$

Can someone come up with an explanation as to why? It's been a few years since I had geometry, and have tried everything I remembered with bisectors and whatnot.

 

[Inspector Gadget]

Forgot to attach the picture...

 

[matt grime]

Here's one way, there are probably several: draw in the perpendicular bisectors from the edge of the triangle to the centre of the circle (ie starting from the points of contact with the circle). The radius is then the altitude of the three new triangles so defined. Ues their areas to work out the area of the large triangle, which you can in turn find using only the lengths of the sides. Benefit of this method: no sin or cosines to work out.

 

[Wooh]

My solution: We can prove that the radius perpendicular to the base also bisects the base (it is on the same line as the perpendicular bisector). So, the base equals 2. The entire perpendicular bisector equals (45)^(1/2) (7^2-2^2=perp^2). Now, we know that the longer sides will also have a tangent radius. This radius will split it into two pieces, one of length 2 and the other of length 5. The piece of length 5 has relation to the perp bisector - the radius. Using the equation of pythagoras, 5^2+r^2=((45)^(1/2)-r)^2
Simplifying will give you your answer.

 

[ahrkron]

Another solution: using two congruent triangles:
T1. Top vertex (A), base midpoint (B), right vertex (C),
T2. Top vertex (A), circle's center (D), intersection between the circle and AC (call this intersection E).

Then, DE/EA = CB/BA.

And you know that: DE is the radius, EA=7-2=5, CB=2, BA=sqrt(45). Solve for r (or DE), substitute, done.

 

[Genza]

Quick question on an old thread, how do Wooh and ahrkron know that the radius tangent to the longer side will split the side into segments of 5 and 2?

 

[Kittel Knight]

Quick question on an old thread, how do Wooh and ahrkron know that the radius tangent to the longer side will split the side into segments of 5 and 2?

The smallest segment equals the half of the triangle's base.