- #1
rocket
- 10
- 0
Hi,
I'm not sure how to do this question. Any help would be great.
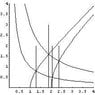
Let B be the region in the first quadrant of [tex] R^2 [/tex] bounded by [tex] xy=1, xy=3, x^2-y^2=1, x^2-y^2=4. [/tex] Find [tex] \int_B(x^2+y^2) [/tex] using the substitution [tex]u=x^2-y^2, v=xy. [/tex]. Use the Inverse Function theorem rather than solving for x and y explicitly.
I'm not sure how to do this question. Any help would be great.
Let B be the region in the first quadrant of [tex] R^2 [/tex] bounded by [tex] xy=1, xy=3, x^2-y^2=1, x^2-y^2=4. [/tex] Find [tex] \int_B(x^2+y^2) [/tex] using the substitution [tex]u=x^2-y^2, v=xy. [/tex]. Use the Inverse Function theorem rather than solving for x and y explicitly.