- #1
symmetric
- 9
- 0
Homework Statement
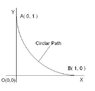
Consider path given by equation [itex] ( x - 1 )^2 + ( y - 1 ) ^2 = 1 [/itex] that connect the points
A = ( 0 , 1 ) and B = ( 1 , 0 ) in xy plane ( shown in image attached ).
A bead falling under influence of gravity from a point A to point B along a curve is given by -
[tex] T = \int \frac{dt}{v}[/tex]
where the bead's velocity is [itex] v = \sqrt{2gy}[/itex] , where g is the gravitational constant.
Homework Equations
[itex] ( x - 1 )^2 + ( y - 1 ) ^2 = 1 [/itex]
The Attempt at a Solution
Given curve [itex] ( x - 1 )^2 + ( y - 1 ) ^2 = 1 [/itex] can be parametrized as -
[itex] x - 1 = \cos\Theta [/itex]
[itex] y - 1 = \sin\Theta [/itex]
curve can be written as
[itex] c( \Theta) = ( 1 + \cos\Theta , 1 + \sin\Theta )[/itex]
[itex] c'( \Theta) = ( - \sin\Theta , \cos\Theta ) [/itex]
[itex] \left| c'( \Theta) \right| = 1 [/itex]
From given relation we have -
[tex]T = \int \frac{dt}{v}[/tex]
[tex]T = \int_{c} \frac{ \left| c'( \Theta) \right| d\Theta}{ \sqrt{2gy}} [/tex]
[tex]T = \int_{\pi}^{ \frac{3\pi}{2}} \frac{d\Theta}{ \sqrt{2g( 1 + \sin\Theta)}} [/tex]
[tex] As, 1 + \sin\Theta = \left( \cos\frac{\Theta}{2} + \sin\frac{\Theta}{2} \right) ^2 [/tex]
[tex]T = \frac{1}{ \sqrt{2g}} \int_{\pi}^{\frac{3\pi}{2}} \frac{d\Theta}{ \cos\frac{\Theta}{2} + \sin\frac{\Theta}{2}} [/tex]
Changing variables ,
[tex] \frac{\theta}{2} = x , d\Theta = 2 dx [/tex]
[tex]T = \frac{1}{ \sqrt{2g}} \int_{\frac{\pi}{2}}^{\frac{3\pi}{4}} \frac{ 2 dx }{ \cos x + \sin x } [/tex]
[tex] As, \sin\frac{\pi}{4} = \cos\frac{\pi}{4} = \frac{1}{\sqrt{2}} [/tex]
multiplying Nr and Dr by [itex]\frac{1}{\sqrt{2}} [/itex]
[tex]T = \frac{1}{\sqrt{g}} \int_{\frac{\pi}{2}}^{\frac{3\pi}{4}} \frac{dx}{ \sin\frac{\pi}{4}\cos x + \cos\frac{\pi}{4} \sin x }[/tex]
[tex]T = \frac{1}{\sqrt{g}} \int_{ \frac{\pi}{2} } ^ {\frac{3\pi}{4}} \frac{dx} { \sin\left( x + \frac{\pi}{4} \right) } [/tex]
[tex]T = \frac{1}{\sqrt{g}} \int_{\frac{\pi}{2}}^{\frac{3\pi}{4}} \csc \left( x + \frac{\pi}{4} \right) dx[/tex]
[tex]T = \frac{1}{\sqrt{g}} \left| \ln \left[ \tan \left( \frac{ x + \frac{\pi}{4} } {2} } \right) \right] \right |_{\frac{\pi}{2}}^{\frac{3\pi}{4}} [/tex]
The value of first term after limit substitution is infinity. Here the value of integral i.e. ' time ' should be strictly finite. What is wrong with my solution?