Lagrangian method problem

[klawlor419]

Homework Statement

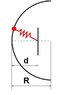
A bead of mass m is free to move on a stationary frictionless hoop of radius R. The hoop is in a horizontal plane (no need to take gravity into account) and it is located a distance d from a stationary wall. The bead is attached to the wall by a spring (constant k and natural length L). Find the frequency of small oscillations about the equilibrium points.

-Just to clarify the problem further, if you draw a line perpendicular to the wall and passing through the diameter of the hoop the point where the line intersects the wall is where the other end of the spring is attached to. The other end is of course attached to the bead.

Homework Equations

the Lagrangian, lagranges equations, kinetic and potential energy of the system. small angle sine and cosine approx's

The Attempt at a Solution

I obtained a solution that makes perfect physical sense, but I did not include the natural length of the spring in my initial solution. my question is does the natural length affect the solution to this problem?
Again the first time I went through this I thought i could simply ignore it because it was a constant, thinking the lagrange equations would make it disappear. Working through it again I realized this was probably not the case, tried solving the equations and ended up with a solution that was a lot uglier.

 

[hikaru1221]

I guess it looks like this? (see picture)
Why don't you show us your work in detail? (it's forum's rule by the way)

 

[klawlor419]

Sorry for the bad description. The wall is outside of the hoop. Other than that though your picture is correct.

So basically the first time I went through the problem i set up the generalized coordinate as the angle between the bead and the horizontal diameter of the hoop. Making my kinetic term m/2*(phi dot squared)*R squared. (Phi beign the angle) Then the potential term is just the elastic potential of the spring which when I worked out the geometry gave me
k/2*[[(R-Rcos(phi)+d)^2+(Rsin(phi))^2)]^1/2-L]^2. after algebra and applying the lagrange equations you get the equations of motion. the equilibrium points are easy to see as 0 and pi. my equations confirmed that. then at that point i made sine and cos approximations to give me the equations of motion for small angles. then evaluated those in terms of a small displacement angle to find the frequency for which my answer was w^2=2k(R+d)/mR.

Now again the first time I did this problem I did not use L in the potential which obviously makes things a lot easier and I obtained the same frequency of small oscillations doing it both ways. Just different equations of motion. So naturally this made me wonder if i did it right at all.

 

[hikaru1221]

Then your 0 position is my pi position in the picture
I think you should check your answer. If I set L = R = d, then the frequency should be zero, I guess.

k/2*[[(R-Rcos(phi)+d)^2+(Rsin(phi))^2)]^1/2-L]^2

I think it should be $$\frac{k}{2} (\sqrt{(d-(R-Rcos\phi))^2+(Rsin\phi)^2}-L)^2$$

 

[klawlor419]

heres the problem picture

 

[klawlor419]

The way you have your picture drawn I agree with your potential term. And I see what you mean regarding the 0,pi positions. But physically I think we are dealing with two different situations. In the picture you have given I think you are right that when L=R=d the frequency should be zero. You're working inside whereas I'm working outside. In the picture I just posted in the case L=R=d it seems there still would be oscillations about the equilibrium points. It seems that case your talking about, correct me if I am wrong is the situation where spring is attached at the center of the hoop? Which seems to be devoid of any distinct equilibrium points. Maybe I'm missing you're point,please let me know.

 

[vela]

So basically the first time I went through the problem i set up the generalized coordinate as the angle between the bead and the horizontal diameter of the hoop. Making my kinetic term m/2*(phi dot squared)*R squared. (Phi beign the angle) Then the potential term is just the elastic potential of the spring which when I worked out the geometry gave me
k/2*[[(R-Rcos(phi)+d)^2+(Rsin(phi))^2)]^1/2-L]^2. after algebra and applying the lagrange equations you get the equations of motion. the equilibrium points are easy to see as 0 and pi. my equations confirmed that. then at that point i made sine and cos approximations to give me the equations of motion for small angles. then evaluated those in terms of a small displacement angle to find the frequency for which my answer was w^2=2k(R+d)/mR.

I think your potential is correct, but when I used the small-angle approximation, I found a different frequency, one that depends on L, namely

$$\omega^2 = \frac{k}{m}\left(1+\frac{d}{R}\right)\left(1-\frac{L}{d}\right)$$

When L=0, it's essentially your answer except for the factor of 2.

 

[hikaru1221]

The way you have your picture drawn I agree with your potential term. And I see what you mean regarding the 0,pi positions. But physically I think we are dealing with two different situations.

I see, I got the wrong picture twice

My answer is also in the same form as vela's, except it's one half of vela's (oh, calculation... :uhh:). One surprising thing is that the restriction of the approximation is not just that the angle is small. The difference d-L has to be large enough. This is why if we plug d=L into vela's answer, we get back unexpected result. If d=L, our linear approximation model won't work

 

[klawlor419]

Ok thanks a lot guys. I'll have to work through the details again.. I'll post again in the next few days hopefully confirming the results. Thanks again.