Parallel Wires

Touchme

1. The problem statement, all variables and given/known data
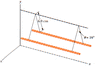
Two long parallel wires, each with a mass per unit length of 43 g/m, are supported in a horizontal plane by 6.0 cm long strings, as shown in Figure P19.64. Each wire carries the same current I, causing the wires to repel each other so that the angle between the supporting strings is 16°.
Determine the magnitude of each current.

2. Relevant equations
sin (theta) = opposite/hyp

I^2 = [(2pi)(d)(mg/L)] / [(4pi)e-07]


3. The attempt at a solution

First I found d (the distance between the wires). Which is 2[sin(8)](0.06m) = 0.0167m.
Then I substitute the given into this equation: I^2 = [(2pi)(d)(mg/L)] / [(4pi)e-07]. I = sq.root of [(2pi)(0.0167)(0.043)(9.8)] / [(4pi)e-07]. the answer I got is 132.64 A. What did I do wrong?

I tried using free body diagram.
T = mg/sin8
Tcos8 = [(I^2)(L)((4pi)e-7)] / [(2pi)d]
(mgcos8)/(sin8) = [(I^2)(L)((4pi)e-7)] / [(2pi)d]
(mg/L)(7.115) = [(I^2)((4pi)e-7)] / [(2pi)0.0167]
I = 159.8 A

Still incorrect.

Attached Thumbnails

 

Touchme

Ah shoot, I've made the most stupid mistake ever. I solved it.