Deflection of locally loaded beam

[diemilio]

Hi everyone,

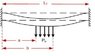
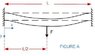
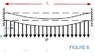
I'm an electrical engineer and I'm trying to find the expression for the deflection of a clamped-clamped beam under a local distributed load. I'm not very familiar with the way the expressions for deflection are obtained, but I've seen that they can be derived in a relative straight-forward fashion. For example, I know that for a clamped-free beam with a point load at the tip, the deflection is given by: w(x) = F*L/(2E*I)*x^2*(1-X/(3L)).

I will really appreciate if someone could please help me out with the expression for deflection as a function of distance for the case of the attached image.

Thanks in advance,

diemilio

 

[Woggy]

This is a statically indeterminate beam. I wasn't sure how to derive the curve out for these beams so I looked it up - you can do it using Macaualy (discontinuous) functions + with super position of the redundant supports. You can look up these terms if you want to try deriving the elastic curve out. I'll try it out later when I have some time.

 

[diemilio]

Hi Woggy,

Thank you for the reply. I've seen people using discontinuous functions and super position but to find the internal shear forces and moments (e.g. "Mechanics of Materials" by Jenkins & Khanna), but I have no idea on how to apply these concepts to solve the differential equation to get the deflection as a function of position.

It really surprises me that the solution to this problem can't be easily found on-line or even in textbooks; I thought that this was a very common problem in mechanics of materials... anyway...

Thanks again for your time and help. I will really appreciate if you could provide me with further insight about the solution to this problem

diemilio

 

[jehake12]

If the length of the applied load to the beam (b-a) is relatively small compared to the overall beam length, then I recommend approximating the distributed load as a point load P at distance D = (b+a)/2. With those criteria, it is relatively simple to do a hand calc using castigliano's method as applied to statically indeterminate beams. Additionally, this peak deflection will be conservative when compared to the actual deflection.

 

[diemilio]

Hi jehake12,

Thanks for the tip but that is not the case... b-a is going to be between 1/2 to 3/4 of the total length of the beam, that's why I need the complete expression.

diemilio

 

[Studiot]

By the looks of your drawing the loading is symmetrical about the centre and your P arrows represent a uniform loading over the length of beam (b-a), rather than a series of point loads.

For a symmetrical case, with the following provisos, the formula you seek is

$$EIy\quad = \quad \left\{ {\frac{{p{L^4}}}{{384}}\; - \;\frac{{p{a^3}}}{{24}}(L - a)} \right\}$$

Where

p is the loading per unit length of a distributed loading
y is the vertical deflection
a is the distance from a support to the start of the loading

The conditions are that the weight of the beam can be neglected
The beam is horizontal or gravity forces can be neglected
The fixed supports do not impose axial forces on the beam although the prevent it rotating.

So if this beam is in an electrical machine p, the beam could be vertical with p applied horizontally and the deflection horizontal.

For a general loading you have a procedure, rather than a formula

Hope this helps

 

[diemilio]

Hi Studiot,

Thank you so much for your reply, but this is not exactly what I'm looking for, but it is very close. I think the expression you're showing is just for the deflection at the center of the beam, whereas I'm looking for a more general expression that gives me y as a function of x.

For instance, I know that if the load was a point load at the center (Figure A) I could express the deflection y(x) as:

$$EIy(x)\quad = \quad \left\{ {\frac{{x^3{(L-x)^3}{F}}}{{3{L^3}}}} \right\}$$

Or if for the same beam I have a distributed load per unit length (Figure B) I can express y(x) as:

$$EIy(x)\quad = \quad \left\{ {\frac{{x^2{(L-x)^2}{P}}}{{24}}} \right\}$$

So what I'm looking for is for a more generalized expression just like the ones above and, if I'm not wrong, for the case I'm interested in, it is probably discontinuous, meaning that for 0<=x<a it will be different than for a<=x<b (and probably b<=x<=L)

Thanks again,

diemilio

 

[hotvette]

I think the ultimate solution is superposition, as has been already mentioned. The loading you have can be considered a combination of uniform loading down across the entire span plus uniform loading across partial span in the opposite directly starting at both ends. My 1967 copy of Roark has this scenario, but only lists the formula for max deflection, not as a function of x. The deflection formula for partial span uniform loading w/ fixed ends must be more difficult than it seems.

Another (perhaps practical) approach is to consider the superposition of a series of point loads (to represent the mid span uniform loading). My guess is that the result will converge relatively quickly as you increase the number of point loads. Messy, but should work. Great task for the computer.

 

[diemilio]

Hi hotvette,

Thanks for the reply. I agree that superposition + discontinuous functions is the way to go but, honestly, I don't have the time nor the experience to derive it myself. I thought this was a very common problem in mechanics and that someone in the forum had already derived a close form expression for it. Anyway, maybe someone has already derived it, but hasn't seen the post yet... I'll keep my fingers crossed

 

[Studiot]

Deriving the midpoint deflection for the symmetrical case is easy because the slope of the elastic curve is zero here, so you don't need to derive an expression for the whole elastic curve just to get the max deflection, which is what is normally required. To get the full curve you need to set up and solve the differential equation.

Hopefully I will have time to do this tomorrow if no one else has posted by then.

 

[diemilio]

Hi Studiot,

Thanks again for the reply. I understand the complexity of the problem and I really appreciate your efforts to help me out!

diemilio

 

[Woggy]

Okay, i worked on it this morning for a while. I did not assume any symmetry. The expression i came up with is verrrryyyy long ...

I've attached a PDF of my attempt to verify if it's correct (i just used some 'typical' values). The entire elastic curve is given by v₁+v₂+v₃, so just piece them together to get the entire elastic curve. $$\Phi$$ is the Heaviside function. k₁ and k₂ are constants that are defined by v₃ and its derivative V₃ (note the capital :P). So to get the entire elastic curve, you'll need to calculate k₁,k₂ and then M and R from those, and then sub M,R in.

I compared my expression with an expression from my textbook that has the load spread across the entire beam (a=0, b=L), and plotted the difference between them at the end of the second page in the PDF. There is error between them, but its very small, around 10^-10 metres. I'm guessing this is because of precision issues.

M*P represents the reaction moment on the right hand side of the beam, which I compared to another example in my textbook (the load is on one half of the beam) and I got the same value.

tl;dr I'm *fairly sure* this is correct, but no guarantees :P also I am only a student, so maybe i shouldn't be trusted :)

 

[diemilio]

hahaha, thank you so much Woggy! I'll try to verify the validity of your expression using FEM software tomorrow morning and I'll let you know how accurate it is. I'm sure is going to turn out just fine; I trust students more than anyone else cause they're the ones with the most recent experience in theoretical analysis; don't you think?? :)

Thanks again,

diemilio

 

[Studiot]

Here is an analytical derivation of your elastic curve.
I said it was a procedure rather than a formula. This is because it is easier to put real numbers in for a real beam and most of the algebra falls away.

In the attachment I have set up the second order controlling differential equation and integrated it twice.

You will see that the trick is to continue the distributed loading to the end of the beam and then apply a second balancing loading in the opposite direction to cancel out the last part.

By suitable choice of coordinate system I have eliminated the constants of integration.
However the resulting equations contain Macauly brackets shown < >. This notation allows the equations to extend the whole length of the beam so we can integrate over the whole length of the beam. Values are only counted if the expresion in the bracket evaluates to a positive value.

This produces two linear equations with two unknowns, the vertical reaction or shear at A and the fixing moment at A.
Once we put real numbers from a real beam into the equations the Macauly brackets become ordinary ones.
So using the condition that there is zero deflection and horizontal slope (=0) also at B we can substitute values for L, a and b to obtain

$$\begin{array}{l} {M_A}L\; + \;\frac{{{V_A}{L^2}}}{2}\; - \;\frac{{p{{(L - a)}^3}}}{6}\; + \;\frac{{p{{(L - b)}^3}}}{6} = \;0 \\ \frac{{{M_A}{L^2}}}{2}\; + \;\frac{{{V_A}{L^3}}}{6}\; - \;\frac{{p{{(L - a)}^4}}}{{24}}\; + \;\frac{{p{{(L - b)}^4}}}{{24}} = \;0 \\ if\quad loading\quad symmetrical \\ a = \;(L - b) \\ \end{array}$$

Solving these simultaneously for $${M_A}$$ and $${{V_A}}$$ and substituting these values into the last equation in the attachment will yield a curve for EIy as a function of x - The required elastic curve.

If the loading is not symmetrical to will need to solve for the reactions at B, using normal mechaics, as well to complete the equation of the curve.

If you would like to do the algebra for a symbolic formula it should be possible and you are very welcome, but you can perhaps see why it is not normally attempted.

 

[diemilio]

Awesome! Thank you so much Studiot! I really like the way you explain how the procedure goes! Let me put together a Matlab file and plot both your solution, Woggy's solutions, and FEM results to see how they look.

I can't tell you how much I appreciate your effort!

diemilio

 

[Studiot]

Any questions, please ask. I did test my algebra on some known solutions.

With L=12; a=3; b=9; p=200 (symmetrical loading)

V = 600 and M = 1650 at each end.

 

[diemilio]

Hi Everyone,

So I plotted Studiot's and Woogy's expressions and they are exactly equal. I also plotted the deflection given by ANSYS and the results look pretty good. There's a very small error between FEM results and the theoretical expressions, but I guess this is due to the plane stress approximation. I'm very very happy with these results and I'm very grateful for all your help.

Please find attach the solutions for a beam with the following characteristics:
L = 600e-6 m, a = 150e-6 m, b = 450e-6 m, P = 25e-3 N/m, E=169e9 Pa, I=0.72e-21 m^4

The green line is for ANSYS Results, Blue line for Studiot's expression, Red line for Woogy's. Max deflection for Studiot's and Woogy's was 7.5120e-9 m; ANSYS showed max deflection of 7.4092e-9 m.

Sorry for the weird dimension sizes; I work in MEMS so dimensions are usually in the nano to micro-meter range.

Again, thanks for all your help and efforts,

diemilio

 

[Studiot]

nice

 

[Woggy]

Cool :) Glad you got what you wanted.

 

[chickencurry]

Diemilio,

Did you use Matlab for FEM? If so, would it be possible for me to see the code?

This would be very much appreciated.

Thanks alot,

Chicken

 

[diemilio]

Hi Chicken,

For FEM I used ANSYS. I used MATLAB to plugin and plot Studiot's and Woggy's equations. Is that the code you want?

diemilio

 

[ashish.mexpert]

Hi Studiot !

The formula given by you is perfectly matching to my case because i have uniformly distributed load which is at center and also symmetric from both ends.

Can you please tell me in which book i can find this formula and what is the differential equation behind this formula ??

I would really appreciate your help

Thanks !

By the looks of your drawing the loading is symmetrical about the centre and your P arrows represent a uniform loading over the length of beam (b-a), rather than a series of point loads.

For a symmetrical case, with the following provisos, the formula you seek is

$$EIy\quad = \quad \left\{ {\frac{{p{L^4}}}{{384}}\; - \;\frac{{p{a^3}}}{{24}}(L - a)} \right\}$$

Where

p is the loading per unit length of a distributed loading
y is the vertical deflection
a is the distance from a support to the start of the loading

The conditions are that the weight of the beam can be neglected
The beam is horizontal or gravity forces can be neglected
The fixed supports do not impose axial forces on the beam although the prevent it rotating.

So if this beam is in an electrical machine p, the beam could be vertical with p applied horizontally and the deflection horizontal.

For a general loading you have a procedure, rather than a formula

Hope this helps

 

[ashish.mexpert]

Hi Studiot,
You solution is really helpfull for me i am having the integrated equation which you solved in the paper after putting the values of Ma and Va into the elastic curve equation , i am not getting the equation which you have written above : EIy=[PL^4/384 + Pa^3(L-a)/24] , how can reach to this equation please tell me and also let me know in which book i can find this particular equation. I am having symmetric case and the formula written above is giving me right results but i want to prove it myself so please help me out. Thank You !