- #1
d.almont23
- 1
- 0
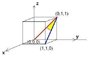
Find the angle between the diagonal of the back and left faces of a cube with one vertex on the origin
A) 60 degrees
B) cos^-1(1/sqrt(6))
C) cos^-1(1/3*sqrt(2))
D) 90 degrees
E) 120 degrees
The two diagonals eminate from the vertex at the origin.
I will write to mean the "norm" of u and u*v to be u "dot" v
I know we have the formula cos(theta) = u*v/( [v]).
But we do not know know any points on the cube so we can't form any vectors...
But since these are the diagonals of a cube they should be the same size . It which case u = v
Then u*v = u^2 and = [v] which impies [v] = u^2. Then cos(theta) = 1 which implies theta = 0 which is definitely not the case...
My other thought is that if these are diagonals on the face of a cube, shouldn't they bisect the 90 degree angles of the cube into 45 degree angles? Then the angle between the two vectors would be 45 + 45 = 90 degrees choice D).
Is this correct?
A) 60 degrees
B) cos^-1(1/sqrt(6))
C) cos^-1(1/3*sqrt(2))
D) 90 degrees
E) 120 degrees
The two diagonals eminate from the vertex at the origin.
I will write to mean the "norm" of u and u*v to be u "dot" v
I know we have the formula cos(theta) = u*v/( [v]).
But we do not know know any points on the cube so we can't form any vectors...
But since these are the diagonals of a cube they should be the same size . It which case u = v
Then u*v = u^2 and = [v] which impies [v] = u^2. Then cos(theta) = 1 which implies theta = 0 which is definitely not the case...
My other thought is that if these are diagonals on the face of a cube, shouldn't they bisect the 90 degree angles of the cube into 45 degree angles? Then the angle between the two vectors would be 45 + 45 = 90 degrees choice D).
Is this correct?